练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在海岸处发现北偏东方向，距处海里的处有一艘走私船.在处北偏西方向，距处海里的处的我方缉私船奉命以海里小时的速度追截走私船，此时走私船正以海里小时的速度从处向北偏东方向逃窜.问：缉私船沿什么方向行驶才能最快截获走私船？并求出所需时间.

    【答案】缉私船应沿北偏东的方向行驶，才能最快截获走私船，大约需要分钟.

    【解析】

    设缉私船追上走私船需小时，进而可表示出和，进而在中利用余弦定理求得，进而在中，根据正弦定理可求得的值，进而求得进而求得，进而利用求得．

    如图，设缉私船应沿方向行驶小时，才能最快截获走私船（在点），

    则海里，海里，

    在中，由余弦定理，得

    ，

    解得.

    又，

    ，

    ，故点在点的正东方向上，

    ，

    在中，由正弦定理，得，

    .

    ，

    缉私船沿北偏东的方向行驶.

    又在中，，，

    ，，即，

    解得小时分钟.

    缉私船应沿北偏东的方向行驶，才能最快截获走私船，大约需要分钟.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知是定义在[-1,1]上的奇函数，且，若任意的，当时，总有．

    （1）判断函数在[-1,1]上的单调性，并证明你的结论；

    （2）解不等式：；

    （3）若对所有的恒成立，其中（是常数），求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率e= ，左、右焦点分别为F1、F2 ， 定点，P（2， ），点F2在线段PF1的中垂线上．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设直线l：y=kx+m与椭圆C交于M、N两点，直线F2M、F2N的倾斜角分别为α、β且α+β=π，求证：直线l过定点，并求该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是不小于3的正整数，集合，对于集合中任意两个元素，.

    定义1：.

    定义2：若，则称，互为相反元素，记作，或.

    （Ⅰ）若，，，试写出，，以及的值；

    （Ⅱ）若，证明：；

    （Ⅲ）设是小于的正奇数，至少含有两个元素的集合，且对于集合中任意两个不相同的元素，，都有，试求集合中元素个数的所有可能值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆Γ： + =1（a＞b＞0）的离心率与双曲线x2﹣y2=a2的离心率之和为 ，B1、B2为椭圆Γ短轴的两个端点，P是椭圆Γ上一动点（不与B1、B2重合），直线B1P、B2P分别交直线l：y=4于M、N两点，△B1B2P的面积记为S1 ， △PMN的面积记为S2 ， 且S1的最大值为4 ．
    （1）求椭圆Γ的方程；
    （2）若S2=λS1 ， 当λ取最小值时，求点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： + =1（a＞b＞0）的焦点为F1 ， F2 ， 离心率为 ，点P为其上动点，且三角形PF1F2的面积最大值为 ，O为坐标原点．
    （1）求椭圆C的方程；
    （2）若点M，N为C上的两个动点，求常数m，使 =m时，点O到直线MN的距离为定值，求这个定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC中，角A，B，C的对边分别为a，b，c，且三角形的面积S= accosB．
    （1）求角B的大小；
    （2）若a=2 ，点D在AB的延长线上，且AD=3，cos∠ADC= ，求b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】牛顿法求方程f（x）=0近似根原理如下：求函数y=f（x）在点（xn ， f（xn））处的切线y=f′（xn）（x﹣xn）+f（xn），其与x轴交点横坐标xn+1=xn﹣ （n∈N*），则xn+1比xn更靠近f（x）=0的根，现已知f（x）=x2﹣3，求f（x）=0的一个根的程序框图如图所示，则输出的结果为（ ）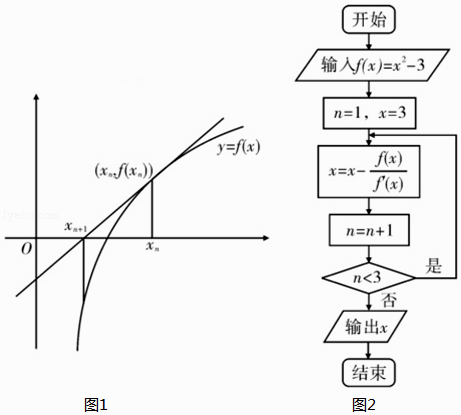
    A.2
    B.1.75
    C.1.732
    D.1.73

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ﹣2cosθ﹣6sinθ+ =0，直线l的参数方程为 （t为参数）．
    （1）求曲线C的普通方程；
    （2）若直线l与曲线C交于A，B两点，点P的坐标为（3，3），求|PA|+|PB|的值．

    查看答案和解析>>

    同步练习册答案