Question

在△ABC中，若sinA=2sinBcosC，sin²A=sin²B+sin²C，则△ABC的形状是（ ）
A．等边三角形
B．等腰三角形
C．直角三角形
D．等腰直角三角形

Answer 1

【答案】分析：通过正弦定理判断出三角形是直角三角形，通过sinA=2sinBcosC，利用正弦定理与余弦定理，推出三角形是等腰三角形，得到结果．
解答：解：因为sin²A=sin²B+sin²C，由正弦定理可知，a²=b²+c²，三角形是直角三角形．
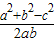
又sinA=2sinBcosC，所以a=2b，解得b=c，三角形是等腰三角形，
所以三角形为等腰直角三角形．
故选D．
点评：本题考查三角形的形状的判断，正弦定理与余弦定理的应用，考查计算能力．