
某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
(1)系统抽样;(2)甲
解析试题分析:(1)这个抽样是在自动包装传送带上每隔30分钟抽取一包产品,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样;
(2)做出两组数据的平均数和方差,把两组数据的方差和平均数进行比较,看出平均数相等,而甲的方差小于乙的方差,得到甲车间比较稳定.
试题解析:(1)甲、乙两组数据间隔相同,所以采用的方法是系统抽样.
(2)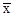 甲=
甲=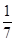 (102+101+99+98+103+98+99)=100,
(102+101+99+98+103+98+99)=100,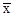 乙=
乙=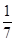 (110+115+90+85+75+115+110)=100,
(110+115+90+85+75+115+110)=100,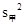 =
=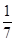 (4+1+1+4+9+4+1)≈3.428 57,
(4+1+1+4+9+4+1)≈3.428 57,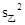 =
=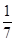 (100+225+100+225+625+225+100)=228.57,
(100+225+100+225+625+225+100)=228.57,
∴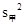 <
<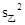 ,故甲车间产品比较稳定.
,故甲车间产品比较稳定.
考点:1.系统抽样;2.样本平均数与方差.


科目:高中数学 来源: 题型:解答题
某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组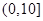 ,第2组
,第2组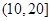 ,第3组
,第3组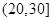 ,第4组
,第4组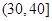 ,第5组
,第5组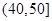 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示. 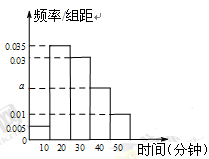
(1)根据图中数据求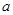 的值
的值
(2)若从第3,4,5组中用分层抽样的方法抽取6名新生参与交通安全问卷调查,应从第3,4,5组
各抽取多少名新生?
(3)在(2)的条件下,该校决定从这6名新生中随机抽取2名新生参加交通安全宣传活动,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y /颗 | 23 | 25 | 30 | 26 | 16 |
 =bx+a;
=bx+a;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某大学联盟的自主招生考试中,报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如下图所示,本次考试中成绩在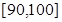 内的记为
内的记为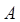 ,其中“语文”科目成绩在
,其中“语文”科目成绩在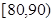 内的考生有10人.
内的考生有10人.
(1)求该考场考生数学科目成绩为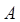 的人数;
的人数;
(2)已知参加本考场测试的考生中,恰有2人的两科成绩均为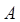 .在至少一科成绩为
.在至少一科成绩为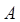 的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为
的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为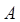 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
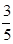 .
.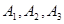 还喜欢打羽毛球,
还喜欢打羽毛球,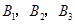 还喜欢打乒乓球,
还喜欢打乒乓球,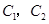 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求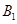 和
和 不全被选中的概率.
不全被选中的概率. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
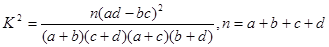 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢 | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
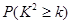 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
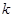 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
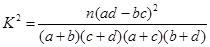 ,其中
,其中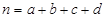 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
空气质量指数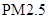 (单位:
(单位: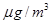 )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
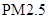 日均浓度 日均浓度 |  | 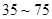 | 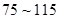 | 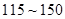 | 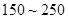 |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
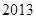 年
年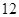 月
月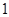 日—
日—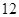 月
月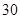 日(
日(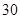 天)对空气质量指数
天)对空气质量指数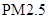 进行监测,获得数据后得到如下条形图.
进行监测,获得数据后得到如下条形图. 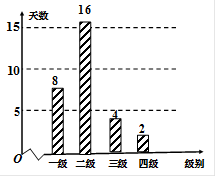
 个,求恰好有一天空气质量类别为中度污染的概率.
个,求恰好有一天空气质量类别为中度污染的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com