(1)x与y之间有很强的线性相关关系,因而可求回归直线方程
(2) =0.668x+54.96
=0.668x+54.96
(3)189分
解析解:(1)列出下表:
i
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
|
xi
| 10
| 20
| 30
| 40
| 50
| 60
| 70
| 80
| 90
| 100
|
yi
| 62
| 68
| 75
| 81
| 89
| 95
| 102
| 108
| 115
| 122
|
xiyi
| 620
|
练习册系列答案
相关习题
科目:高中数学
来源:
题型:解答题
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如下茎叶图所示:
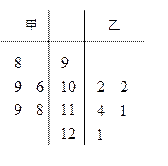
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2) 从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如下关系:
x
| 35
| 40
| 45
| 50
| y
| 56
| 41
| 28
| 11
|
(1)画出散点图,并判断y与x是否具有线性相关关系? (2)求日销售量y对销售单价x的线性回归方程; (3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
| A1
| A2
| A3
| A4
| A5
| 质量指标(x,y,z)
| (1,1,2)
| (2,1,1)
| (2,2,2)
| (1,1,1)
| (1,2,1)
| 产品编号
| A6
| A7
| A8
| A9
| A10
| 质量指标(x,y,z)
| (1,2,2)
| (2,1,1)
| (2,2,1)
| (1,1,1)
| (2,1,2)
|
(1)利用上表提供的样本数据估计该批产品的一等品率; (2)在该样品的一等品中,随机抽取两件产品, (1)用产品编号列出所有可能的结果; (2)设事件 B为“在取出的2件产品中,每件产品的综合指标 S都等于4”,求事件 B发生的概率
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: = = x+ x+ ,使代数式[y1-( ,使代数式[y1-( x1+ x1+ )]2+[y2-( )]2+[y2-( x2+ x2+ )]2+[y3-( )]2+[y3-( x3+ x3+ )]2的值最小时, )]2的值最小时, = = - -  , , = =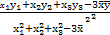 ( ( , , 分别是这三组数据的横、纵坐标的平均数), 分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
x
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| y
| 4
| 6
| 5
| 6.2
| 8
| 7.1
| 8.6
|
(1)求上表中前3组数据的回归直线方程. (2)若|y i-(  x i+  )|≤0.2,即称(x i,y i)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
查看答案和解析>>
|

 =0.668x+54.96
=0.668x+54.96

全优课堂满分备考系列答案
专题王系列答案
学考联通寒假作业冲刺中考长江出版社系列答案
必胜课课课达标系列答案
非常考生课时高效作业本 系列答案

实验班提优辅导教程系列答案

一通百通同步训练系列答案
必胜课小学同步训练系列答案
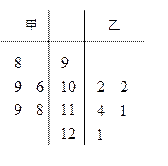
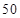 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为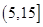 ,
,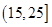 ,
,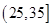 ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图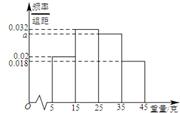
 的值;
的值; 组的频率为
组的频率为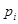 ,第
,第 组区间的中点值为
组区间的中点值为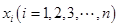 ,则样本数据的平均值为
,则样本数据的平均值为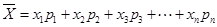 .)
.) 个小球,其中重量在
个小球,其中重量在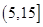 内的小球个数为
内的小球个数为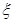 ,求
,求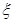 的分布列和数学期望.
的分布列和数学期望.
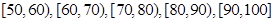 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 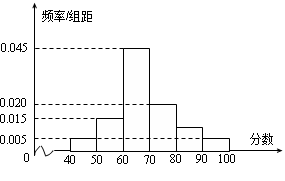
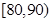 的频率;
的频率;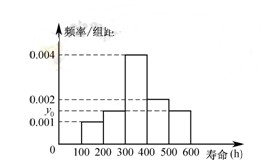
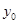 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取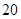 个元件,元件寿命落在
个元件,元件寿命落在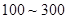 之间的应抽取几个?
之间的应抽取几个?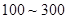 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在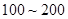 之间,一个元件寿命落在
之间,一个元件寿命落在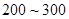 之间”的概率.
之间”的概率. =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=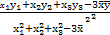 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数), xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.