
某校高一年级60名学生参加数学竞赛,成绩全部在40分至100分之间,现将成绩分成以下6段: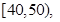
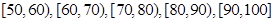 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 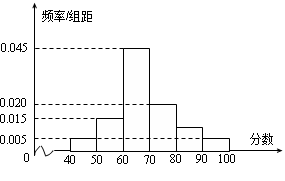
(1)求成绩在区间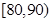 的频率;
的频率;
(2)从成绩大于等于80分的学生中随机选3名学生,其中成绩在[90,100]内的学生人数为ξ,求ξ的分布列与均值.
(1) ;(2)分布列详见解析,
;(2)分布列详见解析,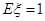 .
.
解析试题分析:本题主要考查频率分步直方图和离散型随机变量的分布列和数学期望等数学知识,考查学生的读图能力、分析问题和解决问题的能力、计算能力.第一问,利用频率分布直方图可知,所有频率之和为1,所有可以求出成绩在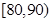 的频率;第二问,通过频率分布直方图分别求出
的频率;第二问,通过频率分布直方图分别求出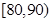 和
和 内的学生人数,先列出
内的学生人数,先列出 的可能取值,再分别求出每一种情况下的概率列出分布列,利用
的可能取值,再分别求出每一种情况下的概率列出分布列,利用 求数学期望.
求数学期望.
试题解析:(1)因为各组的频率之和为1,所以成绩在区间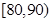 的频率为
的频率为 , 3分
, 3分
(2)由已知和(1)的结果可知成绩在区间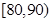 内的学生有
内的学生有 人,
人,
成绩在区间 内的学生有
内的学生有 人, 4 分
人, 4 分
依题意,ξ可能取的值为0,1,2,3 5 分
所以ξ的分布列为ξ 0 1 2 3 P 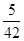



10分
则均值Eξ= 12分
12分
考点:1.频率分布直方图;2.离散型随机变量的分布列和数学期望.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
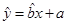 .
. ,你可得到什么结论?
,你可得到什么结论?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.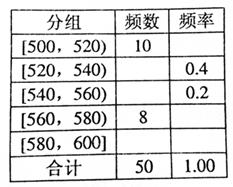
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的被淘汰.若有500人参加测试,学生成绩的频率分布直方图如图.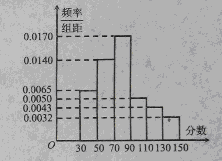
(1)求获得参赛资格的人数;
(2)根据频率直方图,估算这500名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为 ,求甲在初赛中答题个数
,求甲在初赛中答题个数 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
| 区间 |  |  |  |  |  |
| 人数 |  | a | b | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com