
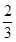 和
和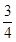 假设两人射击是否击中目标,相互
假设两人射击是否击中目标,相互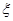 表示甲击中目标时射击的次数,求
表示甲击中目标时射击的次数,求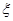 的数学期望
的数学期望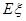 .(结果可以用分数表示)
.(结果可以用分数表示) 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源:不详 题型:解答题
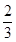 ,被乙小组攻克的概率为
,被乙小组攻克的概率为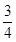 ,
,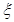 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求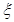 的分布列及数学期望
的分布列及数学期望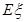 ;
;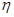 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数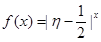 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com