
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
 连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162dm2(版心是指图中的长方形阴影部分,dm为长度单位分米),上、下两边各空2dm,左、右两边各空1dm.
连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162dm2(版心是指图中的长方形阴影部分,dm为长度单位分米),上、下两边各空2dm,左、右两边各空1dm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | $1:\sqrt{2}$ | C. | 2:1 | D. | (π-2):2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
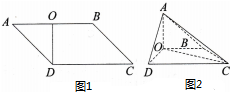 如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.
如图1,在∠A=45°的平行四边形ABCD中,DO垂直平分AB,且AB=2,现将△ADO沿DO折起(如图2),使AC=$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com