
���� ����=4sin�ȿ��Ի�Ϊ��2=4��sin�ȣ����û�����ʽ���ɵó�ֱ�����귽�̣�
����ֱ��l����P����P��ԲC�ڣ��ɵ�|PA|+|PB|=|AB|��
����һ����ֱ��l�IJ������̻�Ϊֱ�����귽��Ϊx-y+1=0�����Բ�ģ�0��2����ֱ��l�ľ���d�������ҳ���ʽ|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$��
����������ֱ��l�IJ������̴���x2+y2-4y=0�У��ɵ�${t^2}-\sqrt{2}t-3=0$�����ø���ϵ���Ĺ�ϵ���ҳ���ʽ���ɵó���
��� �⣺����=4sin�ȿ��Ի�Ϊ��2=4��sin�ȣ���x2+y2-4y=0��Բ��Ϊ��0��2�����뾶Ϊ2��
����ֱ��l����P����P��ԲC�ڣ�����|PA|+|PB|=|AB|��
����һ��$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��Ϊֱ�����귽��Ϊx-y+1=0��
Բ�ģ�0��2����ֱ��l�ľ���Ϊ$\frac{|0-2+1|}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$������$|AB|=2\sqrt{{2^2}-{{��\frac{{\sqrt{2}}}{2}��}^2}}=\sqrt{14}$��
�������� $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$������x2+y2-4y=0��
�ɵ�${t^2}-\sqrt{2}t-3=0$����÷���������Ϊt1��t2��
��t1+t2=$\sqrt{2}$��t1t2=-3��
��|AB|=|t1-t2|=$\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{2-4����-3��}$=$\sqrt{14}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡�ֱ�߲������̵�Ӧ�á��㵽ֱ�ߵľ��빫ʽ���ҳ���ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
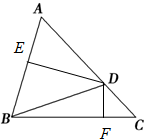 ��ͼ����ABC�У�sin$\frac{1}{2}$��ABC=$\frac{{\sqrt{3}}}{3}$��AB=2����DΪ�߶�AC��һ�㣬��D��DE��ֱ��AB��E����DF��ֱ��BC��F��
��ͼ����ABC�У�sin$\frac{1}{2}$��ABC=$\frac{{\sqrt{3}}}{3}$��AB=2����DΪ�߶�AC��һ�㣬��D��DE��ֱ��AB��E����DF��ֱ��BC��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ȷ | B�� | ��ǰ���ȷ | C�� | Сǰ���ȷ | D�� | ȫ����ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���ķμ��� | �����ķμ��� | �ϼ� | |
| ����40�� | 16 | ||
| С�ڵ���40�� | 12 | ||
| �ϼ� | 40 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 3 | C�� | 5 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com