
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
分析 构造函数${y_1}={x^2}+\frac{2}{x},{y_2}=alnx(a>0)$,由函数$f(x)={x^2}+\frac{2}{x}-alnx(a>0)$有唯一零点x0,则y1,y2有公切点,由此求x0的解析式,即可求出m、n的值.
解答 解:令${y_1}={x^2}+\frac{2}{x},{y_2}=alnx(a>0)$,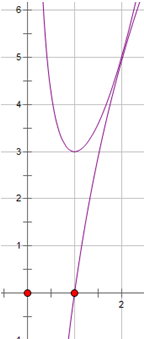
则${y_1}^′=2x-\frac{2}{x^2}=\frac{{2{x^3}-2}}{x^2},{y_2}^′=\frac{a}{x}(a>0,x>0)$,
在(0,1)上y1为减函数,在(1,+∞)上y1为增函数,
所以y1为凹函数,而y2为凸函数;
∵函数$f(x)={x^2}+\frac{2}{x}-alnx(a>0)$有唯一零点x0,
∴y1,y2有公切点(x0,y0),
则$\left\{\begin{array}{l}{{2x}_{0}-\frac{2}{{{x}_{0}}^{2}}=\frac{a}{{x}_{0}}}\\{{{x}_{0}}^{2}+\frac{2}{{x}_{0}}=al{nx}_{0}}\end{array}\right.$,
消去a,得${{x}_{0}}^{2}$+$\frac{2}{{x}_{0}}$-2(${{x}_{0}}^{2}$-$\frac{1}{{x}_{0}}$)lnx0=0;
构造函数$g(x)={x^2}+\frac{2}{x}-2({{x^2}-\frac{1}{x}})lnx,({x>0})$,
则$g(2)=4+1-2(4-\frac{1}{2})ln2=5-7ln2$,
欲比较5与7ln2大小,可比较e5与27大小,
∵e5>27,∴g(2)>0,
$g(e)={e^2}+\frac{2}{e}-2({{e^2}-\frac{1}{e}})=-{e^2}+\frac{3}{e}<0$,
∴x∈(2,e);
∴m=2,n=3,∴m+n=5.
点评 本题考查了函数的性质与应用问题,也考查了利用导数研究函数的单调性问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ③①② | C. | ②③① | D. | ②①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
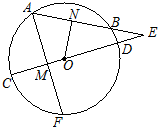 如图,在⊙O中,弦AF交直径CD于点M,弦的延长线交CD的延长线于点E,M、N分别是AF、AB的中点.
如图,在⊙O中,弦AF交直径CD于点M,弦的延长线交CD的延长线于点E,M、N分别是AF、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com