
分析 (Ⅰ)求出函数的导数,计算,f(0),f′(0),求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调性,从而求出函数的最大值即可;
(Ⅲ)求出导数,g(1)=0,可得b=e-$\frac{1}{2}$a-1,得到g(x)=$\frac{1}{2}$ax2+(e-$\frac{1}{2}$a-1)x-ex+1,结合(Ⅱ)运用函数零点存在定理,结合函数的单调性,即可得到所求范围.
解答 解:(Ⅰ)b=0时,f(x)=ax-ex,f′(x)=a-ex,
f(0)=-1,f′(0)=a-1,
故切线方程是:y+1=(a-1)x,
即y=(a-1)x-1;
(Ⅱ)f′(x)=a-ex,
a≤0时,f′(x)<0,f(x)在[0,1]递减,f(x)max=f(0)=b-1;
a>0时,令f′(x)=0,解得:x=lna,
令f′(x)>0,解得:x<lna,令f′(x)<0,解得:x>lna,
f(x)在(-∞,lna)递增,在(lna,+∞)递减,
①lna≤0即0<a≤1时,f(x)在[0,1]递减,f(x)max=f(0)=b-1;
②0<lna<1即1<a<e时,f(x)在[0,lna)递增,在(lna,1]递减,
f(x)max=f(lna)=b-a+alna,
③lna≥1即a≥e时,f(x)在[0,1]递增,
f(x)max=f(1)=b+a-e;
综上,a≤1时,f(x)max=b-1,
1<a<e时,f(x)max=b-a+alna,
a≥e时,f(x)max=b+a-e;
(Ⅲ)g(x)=$\frac{1}{2}$ax2+bx-ex+1,
由g(1)=0,可得b=e-$\frac{1}{2}$a-1,
∴g(x)=$\frac{1}{2}$ax2+(e-$\frac{1}{2}$a-1)x-ex+1,
∴g′(x)=ax+(e-$\frac{1}{2}$a-1)-ex,又g(0)=0.
若函数g(x)在区间(0,1)内有零点,
设x0为g(x)在区间(0,1)内的一个零点,
则由g(0)=g(x0)=0可知,
g(x)在区间(0,x0)内不可能单调递增,也不可能单调递减,
则g′(x)在区间(0,x0)内不可能恒为正,也不可能恒为负.
故g′(x)在区间(0,x0)内存在零点x1.同理g′(x)在区间(x0,1)内存在零点x2.
故函数g(x)在区间(0,1)内至少有三个单调区间,
g′(x)在区间(0,1)内至少有两个零点,
g″(x)=a-ex,
由(Ⅱ)知当a≤1或a≥e时,函数g′(x)在区间[0,1]内单调,
不可能满足“函数g(x)在区间(0,1)内至少有三个单调区间”这一要求.
若1<a<e,此时g′(x)在区间(0,lna)内单调递增,在区间(lna,1)内单调递减.
因此x1∈(0,lna),x2∈(lna,1),
由g′(x)max=g′(lna)=($\frac{a}{2}$+e-1)lna-a+1,
不妨令h(x)=($\frac{x}{2}$+e-1)lnx-x+1,(1<x<e),
则h′(x)=$\frac{1}{2}$lnx+$\frac{e-1}{x}$-$\frac{1}{2}$,h″(x)=$\frac{{x}^{2}-2(e-1)}{{2x}^{2}}$,
令h″(x)>0,解得:x>$\sqrt{2(e-1)}$,令h″(x)<0,解得:x<$\sqrt{2(e-1)}$,
∴h′(x)在(1,$\sqrt{2(e-1)}$)递减,在($\sqrt{2(e-1)}$,e)递增,
∴h′(x)min=h′($\sqrt{2(e-1)}$)=$\frac{1}{2}$[ln$\sqrt{2(e-1)}$+$\sqrt{2(e-1)}$-1]>0,
∴h(x)在(1,e)递增,h(x)>h(1)=0,即g′(x)max>0,
于是,函数g(x)在区间(0,1)内至少有三个单调区间,
只需$\left\{\begin{array}{l}{1<a<e}\\{g′(1)<0}\\{g′(e)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{1<a<e}\\{a+e-\frac{1}{2}a-1-e<0}\\{ae+e-\frac{1}{2}a-1{-e}^{e}<0}\end{array}\right.$,
解得:1<a<2;
故满足条件的a的范围是(1,2).
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查分类讨论的思想方法,考查函数方程的转化思想的运用,属于难题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4}$ | B. | $\frac{π-2}{2}$ | C. | $\frac{π-1}{2}$ | D. | $\frac{π-1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 大于40岁 | 16 | ||
| 小于等于40岁 | 12 | ||
| 合计 | 40 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABEF所在平面与梯形ABCD所在平面互相垂直,且AD⊥AB,DC∥AB,AB=2AD=2CD.
如图,正方形ABEF所在平面与梯形ABCD所在平面互相垂直,且AD⊥AB,DC∥AB,AB=2AD=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
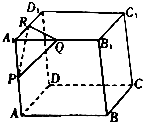 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为( )
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 组距 | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] | (60,70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| A. | $\frac{1}{20}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com