
分析 利用函数是偶函数,求出f(1)=0,然后得出函数的周期,利用函数的周期性,由y=f(x)-loga(x+1)=0得到f(x)=loga(x+1),分别作出函数y=f(x)和y=loga(x+1)的图象,利用图象确定a的取值范围.
解答 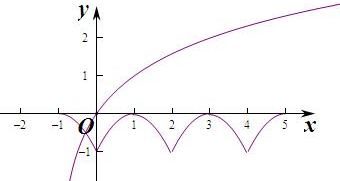 解:∵偶函数f(x)满足对任意x∈R,
解:∵偶函数f(x)满足对任意x∈R,
有f(x+2)=f(x)-f(1),
∴令x=-1得f(-1+2)=f(-1)-f(1),
即f(1)=f(1)-f(1)=0,
则f(x+2)=f(x)-f(1)=f(x),
即函数是周期为2的周期函数,
若x∈[0,1],则x+2∈[2,3],
则f(x)=f(x+2)=-(x-1)2,
当x∈[-1,0],则-x∈[0,1],
∵函数f(x)是偶函数,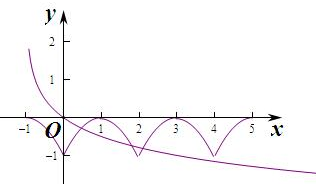
∴f(x)=f(-x)=-(x+1)2,
由y=f(x)-loga(x+1)=0
得到f(x)=loga(x+1),
分别作出函数y=f(x)和
g(x)=loga(x+1)的图象,
若a>1,则不满足条件(图1)
如0<a<1,要使函数y=f(x)-loga(x+1)
在(0,+∞)上至少有三个零点,
则满足当x=2时,f(2)=-1,g(2)>-1,
即loga(2+1)>-1,loga3>-1,
解得0<a<$\frac{1}{3}$.
故答案为:0<a<$\frac{1}{3}$.
点评 本题主要考查函数零点应用,利用数形结合,将方程转化为两个函数图象的相交问题是解决此类问题的基本方法.综合性较强.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A. | O-ABC是正三棱锥(底面为正三角形,顶点在底面的投影为底面的中心) | |
| B. | 直线OB∥平面ACD | |
| C. | OD⊥平面ABC | |
| D. | 直线CD与平面ABC所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
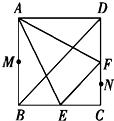 在边长为4cm的正方形ABCD中,E,F分别为BC,CD的中点,M,N分别为AB,CF的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,重合后的点记为B,构成一个三棱锥,则MN与平面AEF的位置关系是MN∥平面AEF.
在边长为4cm的正方形ABCD中,E,F分别为BC,CD的中点,M,N分别为AB,CF的中点,现沿AE,AF,EF折叠,使B,C,D三点重合,重合后的点记为B,构成一个三棱锥,则MN与平面AEF的位置关系是MN∥平面AEF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com