
分析 (1)将A(2,π)、B(2,$\frac{4π}{3}$),分别化为直角坐标为A(2cosπ,2sinπ),B$(2cos\frac{4π}{3},2sin\frac{4π}{3})$,利用斜率计算公式、点斜式即可得出.
(2)利用点到直线的距离公式、三角函数的单调性与值域即可得出.
解答 解:(1)将A(2,π)、B(2,$\frac{4π}{3}$),分别化为直角坐标为A(2cosπ,2sinπ),B$(2cos\frac{4π}{3},2sin\frac{4π}{3})$,
即A,B的直角坐标分别为A(-2,0),B(-1,-$\sqrt{3}$),
kAB=$\frac{-\sqrt{3}-0}{-1+2}$=-$\sqrt{3}$,
∴直线AB的方程为y=-$\sqrt{3}$(x+2),
即AB的方程为$\sqrt{3}$x+y+2$\sqrt{3}$=0.
(2)设M(2cosθ,sinθ),它到直线AB距离d=$\frac{|2\sqrt{3}cosθ+sinθ+2\sqrt{3}|}{2}$=$\frac{|\sqrt{13}sin(θ+φ)+2\sqrt{3}|}{2}$≤$\frac{\sqrt{13}+2\sqrt{3}}{2}$,当sin(θ+φ)=1时取等号.
∴点M到直线AB距离的最大值是$\frac{\sqrt{13}+2\sqrt{3}}{2}$.
点评 本题考查了极坐标化为直角坐标、点斜式、点到直线的距离公式、三角函数的单调性与值域、和差公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 甲乙两名学生六次数学测验成绩(百分制)如图所示.
甲乙两名学生六次数学测验成绩(百分制)如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABEF所在平面与梯形ABCD所在平面互相垂直,且AD⊥AB,DC∥AB,AB=2AD=2CD.
如图,正方形ABEF所在平面与梯形ABCD所在平面互相垂直,且AD⊥AB,DC∥AB,AB=2AD=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
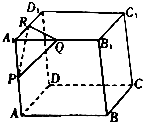 正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为( )
正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com