
| |||||||||||||||
(1) |
解析:设经过原点且倾角为 |
(2) |
S= ①当m>n,即 由于0< ②当m<n,即 因为0<tan 是 所以u= |
(3) |
①当 ②当 又由 综上,当u>mn时, 点评:本题主要考查椭圆的对称性及不等式的应用,通过求最大值来考查逻辑思维能力和应用能力,同时体现分类讨论思想. |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:044
设椭圆的方程为![]() =1(m,n>0),过原点且倾角为θ和π-θ(0<θ<
=1(m,n>0),过原点且倾角为θ和π-θ(0<θ<![]() =的两条直线分别交椭圆于A、C和B、D两点,
=的两条直线分别交椭圆于A、C和B、D两点,
(Ⅰ)用θ、m、n表示四边形ABCD的面积S;
(Ⅱ)若m、n为定值,当θ在(0,![]() ]上变化时,求S的最小值u;
]上变化时,求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)用θ、m、n表示四边形ABCD的面积S;
(Ⅱ)若m、n为定值,当θ在(0,![]() ]上变化时,求S的最小值u;
]上变化时,求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
椭圆的方程为![]() +
+![]() =1,A1、A2分别是椭圆的左、右顶点,P是椭圆上任一点,作A1Q⊥A1P,A2Q⊥A2P,设A1Q与A2Q相交于点Q,求Q点的轨迹方程.
=1,A1、A2分别是椭圆的左、右顶点,P是椭圆上任一点,作A1Q⊥A1P,A2Q⊥A2P,设A1Q与A2Q相交于点Q,求Q点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二圆锥曲线的综合问题练习卷(解析版) 题型:解答题
如图,F是椭圆的右焦点,以点F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆上的动点,P到椭圆两焦点的距离之和等于4.
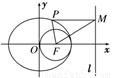
(1)求椭圆和圆的标准方程;
(2)设直线l的方程为x=4,PM⊥l,垂足为M,是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com