
设椭圆的方程为![]() =1(m,n>0),过原点且倾角为θ和π-θ(0<θ<
=1(m,n>0),过原点且倾角为θ和π-θ(0<θ<![]() =的两条直线分别交椭圆于A、C和B、D两点,
=的两条直线分别交椭圆于A、C和B、D两点,
(Ⅰ)用θ、m、n表示四边形ABCD的面积S;
(Ⅱ)若m、n为定值,当θ在(0,![]() ]上变化时,求S的最小值u;
]上变化时,求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范围.
的取值范围.
解:(Ⅰ)设经过原点且倾角为θ的直线方程为y=xtanθ,可得方程组 (Ⅱ)S= (1)当m>n,即 由于0<θ≤ 故tanθ= (2)当m<n,即 由于
因为0<tanθ1<tanθ2≤1,m2tanθ1tanθ2-n2<m2-n2<0,所以(m2tanθ2+ 所以u= (Ⅲ)(1)当 (2)当 所以 得 综上,当u>mn时, |


科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)用θ、m、n表示四边形ABCD的面积S;
(Ⅱ)若m、n为定值,当θ在(0,![]() ]上变化时,求S的最小值u;
]上变化时,求S的最小值u;
(Ⅲ)如果μ>mn,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2007年综合模拟数学卷三 题型:044
设椭圆C1的方程为![]() =1,(a>b>0).曲线C2的方程为y=
=1,(a>b>0).曲线C2的方程为y=![]() .且C1与C2在第一象限内只有一个公共点P.
.且C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A,B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2…yn}为y1,y2…yn中最小的一个,设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a),S(a)}的表达式.
查看答案和解析>>
科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:2010年全国普通高等学校招生统一考试、文科数学(上海卷) 题型:044
已知椭圆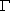 的方程为
的方程为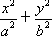 =1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)为
=1(a>b>0),A(0,b)、B(0,-b)和Q(a,0)为 的三个顶点.
的三个顶点.
(1)若点M满足![]() ,求点M的坐标;
,求点M的坐标;
(2)设直线l1∶y=k1x+p交椭圆 于C、D两点,交直线l2∶y=k2x于点E.若k1·k2=
于C、D两点,交直线l2∶y=k2x于点E.若k1·k2= ,证明:E为CD的中点;
,证明:E为CD的中点;
(3)设点P在椭圆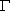 内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆
内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆 的两个交点P1,P2满足
的两个交点P1,P2满足![]() ?令a=10,b=5,点P的坐标是(-8,-1).若椭圆
?令a=10,b=5,点P的坐标是(-8,-1).若椭圆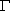 上的点P1,P2满足
上的点P1,P2满足![]() ,求点P1,P2的坐标.
,求点P1,P2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com