
【题目】已知函数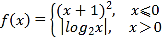 ,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则
,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则![]() 的取值范围为( )
的取值范围为( )
A. (﹣1,+∞)B. (﹣1,1]C. (﹣∞,1)D. [﹣1,1)
【答案】B
【解析】
由方程f(x)=a,得到x1,x2关于x=﹣1对称,且x3x4=1;化简![]() ,利用数形结合进行求解即可.
,利用数形结合进行求解即可.
作函数f(x)的图象如图所示,∵方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,
∴x1,x2关于x=﹣1对称,即x1+x2=﹣2,0<x3<1<x4,则|log2x3|=|log2x4|,
即﹣log2x3=log2x4,则log2x3+log2x4=0,即log2x3x4=0,则x3x4=1;
当|log2x|=1得x=2或![]() ,则1<x4≤2;
,则1<x4≤2;![]() ≤x3<1;
≤x3<1;
故![]() ;
;
则函数y=﹣2x3+![]() ,在
,在![]() ≤x3<1上为减函数,则故当x3=
≤x3<1上为减函数,则故当x3=![]() 取得y取最大值y=1,
取得y取最大值y=1,
当x3=1时,函数值y=﹣1.即函数取值范围是(﹣1,1].
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)设集合C={x|m+1<x<2m-1},若B∩C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是异面直线,给出下列结论:
是异面直线,给出下列结论:
①一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
③一定存在无数个平面![]() ,使直线
,使直线![]() 与平面
与平面![]() 交于一个定点,且直线
交于一个定点,且直线![]() 平面
平面![]() .
.
则所有正确结论的序号为( )
A.①②B.②C.②③D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学届的震动。在1859年的时候,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想。在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,
的结论。若根据欧拉得出的结论,估计1000以内的素数的个数为_________(素数即质数,![]() ,计算结果取整数)
,计算结果取整数)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com