
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)设![]() ,求证:当
,求证:当![]() 时,函数
时,函数![]() 恰有2个不同零点.
恰有2个不同零点.
【答案】(1)![]() (2)单调增区间为
(2)单调增区间为![]() 和
和![]() ;单调减区间为
;单调减区间为![]() 和
和![]() .(3)证明见解析
.(3)证明见解析
【解析】
(1)由![]() ,得
,得![]() ,所以
,所以![]() ,即可求得答案;
,即可求得答案;
(2)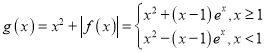 ,根据导数,分别讨论
,根据导数,分别讨论![]() 和
和![]() 函数的单调性,即可求得函数
函数的单调性,即可求得函数![]() 的单调区间;
的单调区间;
(3)因为![]() ,设
,设![]() ,得
,得![]() ,令
,令![]() ,当
,当![]() ,
,![]() ,结合已知和零点定义,即可求得答案.
,结合已知和零点定义,即可求得答案.
(1)由![]() ,得
,得![]() ,
,
![]()
![]() ,
,
![]() 曲线
曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(2)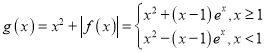 ,
,
当![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() .
.
当![]() 时,
时,![]() ,
,
![]()
![]() ,
,
令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() 或
或![]() ,
,
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]() ;单调减区间为
;单调减区间为![]() 和
和![]() .
.
综上所述,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ;
;
函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
(3)由题意知,![]() ,
,
得![]() ,
,
令![]() ,
,
当![]() 时,
时,![]() ,
,
![]()
![]() 在
在![]() 上单调递增,
上单调递增,
又![]()
![]() ,
,![]() ,
,
![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 是
是![]() 的唯一极值点,
的唯一极值点,
令![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
即当![]() 时,
时,![]() ,即
,即![]() ,
,
![]()
![]()
![]() ,
,
又![]()
![]() ,
,
![]() 函数
函数![]() 在
在![]() 上有唯一的零点,
上有唯一的零点,
又![]()
![]() 在
在![]() 上有唯一的零点,
上有唯一的零点,
![]() 函数
函数![]() 恰有2个不同零点.
恰有2个不同零点.


科目:高中数学 来源: 题型:
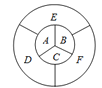
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西光厂眼镜车间接到一批任务,需要加工6000个![]() 型零件和2000个
型零件和2000个![]() 型零件.这个车间有214名工人,他们每一个人加工5个
型零件.这个车间有214名工人,他们每一个人加工5个![]() 型零件的时间可以加工3个
型零件的时间可以加工3个![]() 型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
型零件.将这些工人分成两组,两组同时工作,每组加工一种型号的零件,为了在最短的时间内完成这批任务,应怎样分组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击疫情,中国人民心连心,向世界展示了中华名族的团结和伟大,特别是医护工作者被人们尊敬的称为“最美逆行者”,各地医务工作者主动支援湖北武汉.现有7名医学专家被随机分配到“雷神山”、“火神山”两家医院.
(1)求7名医学专家中恰有两人被分配到“雷神山”医院的概率;
(2)若要求每家医院至少一人,设![]() ,
,![]() 分别表示分配到“雷神山”、“火神山”两家医院的人数,记
分别表示分配到“雷神山”、“火神山”两家医院的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
① 函数![]() 的最小正周期是
的最小正周期是![]() ;
;
② 函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③ 函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
④ 函数![]() 的图像可由函数
的图像可由函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再向下平移1个单位得到.其中正确结论的个数是( )
个单位,再向下平移1个单位得到.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知两个变量线性相关,若它们的相关性越强,则相关系数的绝对值越接近于1.
(2)线性回归直线必过点![]() ;
;
(3)对于分类变量A与B的随机变量![]() ,
,![]() 越大说明“A与B有关系”的可信度越大.
越大说明“A与B有关系”的可信度越大.
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
(5)根据最小二乘法由一组样本点![]() ,求得的回归方程是
,求得的回归方程是![]() ,对所有的解释变量
,对所有的解释变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差.
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com