
下列结论中正确命题的序号是 (写出所有正确命题的序号).
①积分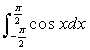 的值为2;②若
的值为2;②若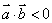 ,则
,则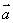 与
与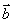 的夹角为钝角;③若
的夹角为钝角;③若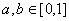 ,则不等式
,则不等式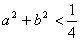 成立的概率是
成立的概率是 ;④函数
;④函数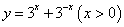 的最小值为2.
的最小值为2.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
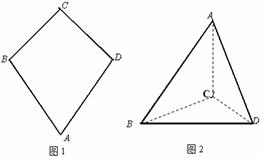
如图一,平面四边形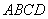 关于直线
关于直线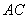 对称,
对称,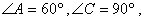
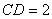 。
。
把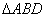 沿
沿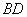 折起(如图二),使二面角
折起(如图二),使二面角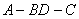 的余弦值等于
的余弦值等于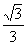 。对于图二,
。对于图二,
(Ⅰ)求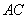 ;(Ⅱ)证明:
;(Ⅱ)证明: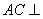 平面
平面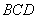 ;
;
(Ⅲ)求直线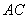 与平面
与平面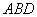 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,射线OA,OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别
交OA,OB于A,B两点,当AB的中点C恰好落在直线y= x上时,求直线AB的方程.
x上时,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com