练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在平面几何里有射影定理：设△ABC的两边AB⊥AC，D是A点在BC边上的射影，则AB2=BD•BC．拓展到空间，在四面体A-BCD中，DA⊥面ABC，点O是A在面BCD内的射影，且O在△BCD内，类比平面三角形射影定理，△ABC，△BOC，△BDC三者面积之间关系为______．
    由已知在平面几何中，
    若△ABC中，AB⊥AC，AE⊥BC，E是垂足，
    则AB2=BD•BC，
    我们可以类比这一性质，推理出：
    若三棱锥A-BCD中，AD⊥面ABC，AO⊥面BCD，O为垂足，
    则（S△ABC）2=S△BOC．S△BDC．
    故答案为：（S△ABC）2=S△BOC．S△BDC
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    某校对文明班的评选设计了五个方面的多元评价指标，并通过经验公式样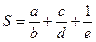来计算各班的综合得分，S的值越高则评价效果越好，若某班在自测过程中各项指标显示出，则下阶段要把其中一个指标的值增加1个单位，而使得S的值增加最多，那么该指标应为        ．（填入中的某个字母）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知二次函数f(x)＝ax2＋bx＋c的图象与x轴有两个不同的交点，若f(c)＝0且0<x<c时，f(x)>0，
    (1)证明：是f(x)＝0的一个根；
    (2)试比较与c的大小；
    (3)证明：－2<b<－1.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    我们知道，在边长为2a的正三角形内任一点到三边的距离之和为定值
    		3
    a    ，类比上述结论，在边长为3a的正四面体内任一点到其四个面的距离之和为定值______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在平面几何中有如下结论：正三角形ABC的内切圆面积为S1，外接圆面积为S2，则
    S1
    S2
    =
    1
    4
    ，推广到空间可以得到类似结论；已知正四面体P-ABC的内切球体积为V1，外接球体积为V2，则
    V1
    V2
    =______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    平面上有n个圆，其中每两个圆之间都相交于两个点，每三个圆都无公共点，它们将平面分成f（n）块区域，则f（n）的表达式是（　　）
    A．2nB．2n-（n-1）（n-2）（n-3）
    C．n3-5n2+10n-4D．n2-n+2

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    可作为四面体的类比对象的是（　　）
    A．四边形B．三角形C．棱锥D．棱柱

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如图，对于大于1的自然数m的n次幂可用奇数进行如图所示的“分裂”，仿此，记53的“分裂”中的最小数为a，而52的“分裂”中最大的数是b，则a+b=______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数在点处的导数是  (     )
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案