【答案】
分析:(Ⅰ)设数列{a
n}的公差为d,数列{b
n}的公比为q(q>0),列关于d与q的方程组求得d与q,即可求得{a
n},{b
n}的通项公式;
(Ⅱ)由c
n+2c
n-1+…+(n-1)c
2+nc
1=2
n+1-n-2向下递推一项可得c
n-1+2c
n-2+…+(n-2)c
2+(n-1)c
1=2
n-(n-1)-2(n≥2),两式相减即可求得c
n=2
n-1(n≥3),再验证n=1,2时的情况即可,符合则合,不符合则分段写.
解答:(Ⅰ)设数列{a
n}的公差为d,数列{b
n}的公比为q(q>0)
由题意得
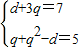
解得
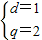
,
∴a
n=n,b
n=3×2
n-1;
(Ⅱ)由c
n+2c
n-1+…+(n-1)c
2+nc
1=2
n+1-n-2
知c
n-1+2c
n-2+…+(n-2)c
2+(n-1)c
1=2
n-(n-1)-2(n≥2)
两式相减:c
n+c
n-1+…+c
2+c
1=2
n-1(n≥2)
∴c
n-1+…+c
2+c
1=2
n-1-1(n≥3)
∴c
n=2
n-1(n≥3)
当n=1,2时,c
1=1,c
2=2,适合上式.
∴c
n=2
n-1(n∈N
*).
即{c
n}是等比数列
点评:本题考查等差数列与等比数列的通项公式,考查数列的求和,突出考查方程组思想、转化思想与分类讨论思想的综合运用,属于中档题.

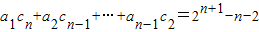 对任意n∈N*都成立;求证:数列{cn}是等比数列.
对任意n∈N*都成立;求证:数列{cn}是等比数列.
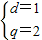 ,
,

 小学教材全测系列答案
小学教材全测系列答案