
若S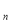 是公差不为0的等差数列
是公差不为0的等差数列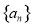 的前
的前 项和,且
项和,且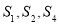 成等比数列。
成等比数列。
(1)求等比数列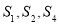 的公比;
的公比;
(2)若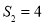 ,求
,求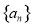 的通项公式;
的通项公式;
(3)设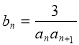 ,
,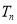 是数列
是数列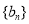 的前
的前 项和,求使得
项和,求使得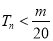 对所有
对所有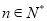 都成立的最小正整数
都成立的最小正整数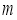 。
。
(1) ;(2)
;(2) ;(3)
;(3)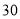
【解析】
试题分析:根据题意设等差数列的首项和公差分别为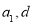 ,同时
,同时 ,再根据
,再根据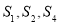 成等比数列,得到
成等比数列,得到 (1)显然
(1)显然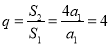 ,求得公比为
,求得公比为 ;(2)根据公式列出关于
;(2)根据公式列出关于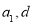 的方程,
的方程, 同时与
同时与 联立,求得
联立,求得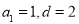 的值,其通项公式
的值,其通项公式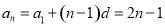 ;(3)根据(2)找到
;(3)根据(2)找到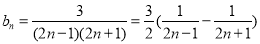 ,利用裂项相消法求其和
,利用裂项相消法求其和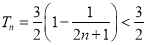 ,须使
,须使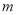 满足
满足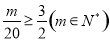 ,
,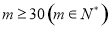 ,进而得到最小正整数
,进而得到最小正整数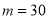 .
.
试题解析:∵数列{an}为等差数列,∴ ,
,
∵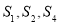 成等比数列, ∴ S1·S4 =S22
成等比数列, ∴ S1·S4 =S22
∴ 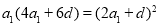 ,∴
,∴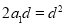
∵公差d不等于0,∴ 5分
5分
(1)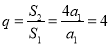 7分
7分
(2)∵S2 =4,∴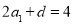 ,又
,又 ,
,
∴ , ∴
, ∴ . 9分
. 9分
(3)∵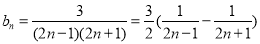
∴
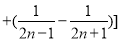
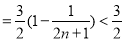 12分
12分
要使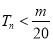 对所有n∈N*恒成立,
对所有n∈N*恒成立,
∴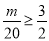 ,
,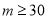 ,
,
∵m∈N*, ∴m的最小值为30。 14分
考点:1.等差数列的公式;2.裂项相消法求和;3.解不等式.


科目:高中数学 来源:2014-2015学年广东省东莞市三校高二上学期期中联考试卷(解析版) 题型:选择题
已知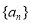 是由正数组成的等比数列,
是由正数组成的等比数列, 表示
表示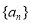 的前
的前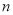 项的和.若
项的和.若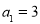 ,
,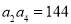 ,
,
则 的值是( )
的值是( )
A.511 B.1023 C.1533 D.3069
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省枣庄市高三1月月考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在平面直角坐标系 中,点
中,点 ,直线
,直线 ,设圆
,设圆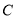 的半径为
的半径为 ,圆心在
,圆心在 上.
上.
(1)若圆心 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆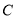 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心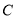 的横坐标
的横坐标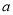 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com