
已知函数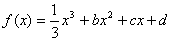 ,设曲线
,设曲线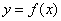 在与
在与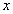 轴交点处的切线为
轴交点处的切线为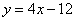 ,
,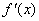 为
为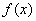 的导函数,满足
的导函数,满足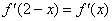 .
.
(1)求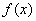 ;
;
(2)设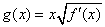 ,
,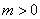 ,求函数
,求函数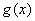 在
在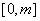 上的最大值;
上的最大值;
(3)设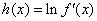 ,若对一切
,若对一切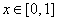 ,不等式
,不等式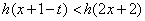 恒成立,求实数
恒成立,求实数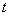 的取值范围.
的取值范围.
解:(1)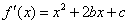 ,
,
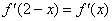 ,
, 函数
函数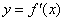 的图像关于直线
的图像关于直线 对称,则
对称,则 .
.

 直线
直线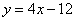 与
与 轴的交点为
轴的交点为 ,
,
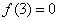 ,且
,且 ,
,
即 ,且
,且 ,
,
解得 ,
, .
.
则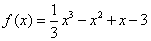 .
.
(2)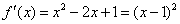 ,
,

其图像如图所示.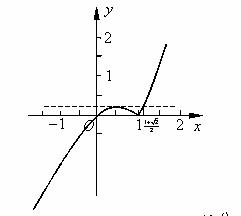
当 时,
时, ,根据图像得:
,根据图像得:
(ⅰ)当 时,
时,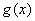 最大值为
最大值为 ;
;
(ⅱ)当 时,
时,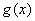 最大值为
最大值为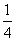 ;
;
(ⅲ)当 时,
时,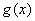 最大值为
最大值为 .
.
(3)方法一: ,
,
 ,
, ,
,
 当
当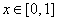 时,
时, ,
,
 不等式
不等式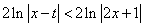 恒成立等价于
恒成立等价于 且
且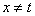 恒成立,
恒成立,
由 恒成立,得
恒成立,得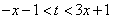 恒成立,
恒成立,
 当
当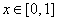 时,
时,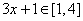 ,
, ,
,

 ,
,
 又
又 当
当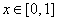 时,由
时,由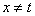 恒成立,得
恒成立,得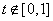 ,
,
因此,实数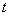 的取值范围是
的取值范围是 .
.
 方法二:(数形结合法)作出函数
方法二:(数形结合法)作出函数 的图像,其图像为线段
的图像,其图像为线段 (如图),
(如图),

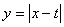 的图像过点
的图像过点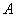 时,
时,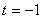 或
或 ,
,
 要使不等式
要使不等式 对
对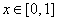 恒成立,
恒成立,
必须 ,
,
又 当函数
当函数 有意义时,
有意义时,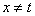 ,
,
 当
当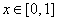 时,由
时,由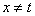 恒成立,得
恒成立,得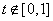 ,
,
因此,实数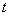 的取值范围是
的取值范围是 .
.
方法三: ,
,  的定义域是
的定义域是 ,
,
 要使
要使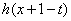 恒有意义,必须
恒有意义,必须 恒成立,
恒成立,

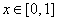 ,
,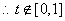 ,即
,即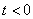 或
或 . ………………①
. ………………①
 由
由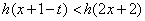 得
得 ,
,
即 对
对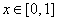 恒成立,
恒成立,
令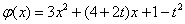 ,
,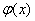 的对称轴为
的对称轴为 ,
,
则有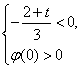 或
或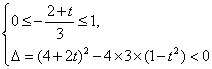 或
或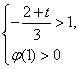
解得 . ………………②
. ………………②
综合①、②,实数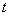 的取值范围是
的取值范围是 .
.


科目:高中数学 来源: 题型:
已知函数f(x)=x3-ax2-bx+a2在x=1处有极值10,则a、b的值为( )
A.a=-4,b=11 B.a=-4,b=1或a=-4,b=11
C.a=-1,b=5 D.以上都不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
一个盒子中装有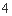 张卡片,每张卡片上写一个数字,数字分别是1、2、3、4.现从盒子中随机抽取卡片.若一次抽取3张卡片,求3张卡片上数字之和大于
张卡片,每张卡片上写一个数字,数字分别是1、2、3、4.现从盒子中随机抽取卡片.若一次抽取3张卡片,求3张卡片上数字之和大于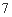 的概率( )
的概率( )
A.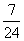 B.
B.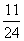 C.
C.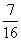 D.
D.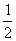
查看答案和解析>>
科目:高中数学 来源: 题型:
若直角坐标平面内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的一个“友好点对”(点对(P,Q)与点对(Q,P)为同一个“友好点对”).已知函数f(x)=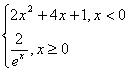 则f(x)的“友好点对”有( )个.
则f(x)的“友好点对”有( )个.
A.0 B.1 C.2 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com