
【题目】已知二次函数![]()
![]() ,
,![]()
(1)若![]() ,且对
,且对![]() ,函数
,函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() 且
且![]() 为偶函数,证明
为偶函数,证明![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(﹣∞,+∞)上的偶函数,x1 , x2∈[0,+∞)(x1≠x2),有 ![]() ,则( )
,则( )
A.f(3)<f(1)<f(﹣2)
B.f(1)<f(﹣1)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(﹣2)<f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图. 
(1)试评估该校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全省前130名的人数记为ξ,求ξ的分布列和数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若a,b∈R,且a+b>4,则a,b至少有一个大于2
B.若p是q的充分不必要条件,则¬p是¬q的必要不充分条件
C.若命题p:“ ![]() >0”,则¬p:“
>0”,则¬p:“ ![]() ≤0”
≤0”
D.△ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
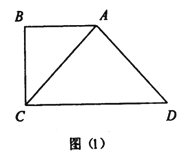
【题目】已知直角梯形![]() ,如图(1)所示,
,如图(1)所示, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图(2)所示.
,如图(2)所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,
(1)试画出f(x),x∈[-3,5]的图象;
(2)求f(37.5);
(3)常数a∈(0,1),y=a与f(x),x∈[-3,5]的图象相交,求所有交点横坐标之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1 . 
(1)求证:A1B⊥AD;
(2)若AD=AB=2BC,∠A1AB=60°,点D在平面ABB1A1上的射影恰为线段A1B的中点,求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com