
【题目】已知函数 ![]() ,若存在x∈N*使得f(x)≤2成立,则实数a的取值范围为 .
,若存在x∈N*使得f(x)≤2成立,则实数a的取值范围为 .
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合.直线l的参数方程是 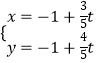 (t为参数),曲线C的极坐标方程为ρ=
(t为参数),曲线C的极坐标方程为ρ= ![]() sin(
sin( ![]() ).
).
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于M、N两点,求M、N两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°. 
(1)证明:CP⊥BD;
(2)若AP=PC=2 ![]() ,求二面角A﹣BP﹣C的余弦值.
,求二面角A﹣BP﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 
(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)若二面角P﹣CD﹣B为45°,AD=2,CD=3,求点F到平面PCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形,若该三棱锥的顶点都在同一球面上,则该球的表面积为( ) 
A.27π
B.48π
C.64π
D.81π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x+b)ex , F(x)=bx﹣lnx,b∈R.
(1)若b<0,且存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,求b的取值范围;
(2)若F(x+1)>b对任意x∈(0,+∞)恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△AnBnCn的三边长分别为an , bn , cn , n=1,2,3…,若b1>c1 , b1+c1=2a1 , an+1=an , bn+1= ![]() ,cn+1=
,cn+1= ![]() ,则∠An的最大值是 .
,则∠An的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com