
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(2)求函数![]() 的极值点;
的极值点;
(3)当![]() 时,试证明对任意的正整数
时,试证明对任意的正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
【答案】(1)函数![]() 在定义域
在定义域![]() 上单调递增(2)答案不唯一,具体见解析(3)详见解析
上单调递增(2)答案不唯一,具体见解析(3)详见解析
【解析】
(1)分析函数定义域,求导数,当![]() 时,
时,![]() 恒成立,即可写出函数单调区间(2)由(1)中
恒成立,即可写出函数单调区间(2)由(1)中![]() ,分
,分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况分类讨论函数的单调性,写出函数极值点(3)观察不等式构造函数
四种情况分类讨论函数的单调性,写出函数极值点(3)观察不等式构造函数![]() ,利用导数可证
,利用导数可证![]() 在
在![]() 上单调递增,可知
上单调递增,可知![]() 恒成立,令
恒成立,令![]() 即可证明.
即可证明.
(1)函数![]() 的定义域为
的定义域为![]() ①,
①,
![]() ,
,
令![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,
,
即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() .
.
即当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上单调递增.
上单调递增.
(2)①由(1)知,当![]() 时,函数无极值点.
时,函数无极值点.
②当![]() 时,
时, ,
,
因为当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上无极值点.
上无极值点.
③当![]() 时,解
时,解![]() ,得
,得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
且![]() 时,
时,![]() ,
,![]() 时,
时,
![]() ,此时
,此时![]() 在
在![]() 上有唯一的极小值点
上有唯一的极小值点![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() ,
,![]() 上都大于0,
上都大于0,![]() 在
在![]() 上小于0,
上小于0,
此时![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() .
.
综上可知,当![]() 时,
时,![]() 在
在![]() 上有唯一的极小值点
上有唯一的极小值点![]() ;
;
当![]() 时,
时,![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上无极值点.
上无极值点.
(3)证明:当![]() 时,
时,![]() ,
,
令![]() ,
,
则![]() ,
,
显然![]() 在
在![]() 上恒为正,
上恒为正,
所以![]() 在
在![]() 上单调递增,即当
上单调递增,即当![]() 时,恒有
时,恒有![]() ,
,
所以当![]() 时,有
时,有![]() ,
,
即![]() ,所以对任意正整数
,所以对任意正整数![]() ,取
,取![]() ,可得
,可得![]() 恒成立.
恒成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.

(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
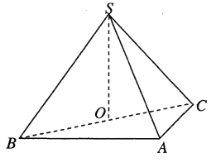
(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在![]() 层班级,生物在
层班级,生物在![]() 层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 | 化学 | 地理 | 化学 |
生物 | 化学 | 生物 | 历史 |
物理 | 生物 | 物理 | 生物 |
物理 | 生物 | 物理 | 物理 |
政治1班 | 物理 | 政治2班 | 政治3班 |
A.8种B.10种C.12种D.14种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为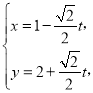 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴为极轴的极坐标系中,圆
轴为极轴的极坐标系中,圆![]() 的方程
的方程![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求弦
两点,求弦![]() 中点
中点![]() 的直角坐标和
的直角坐标和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com