
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
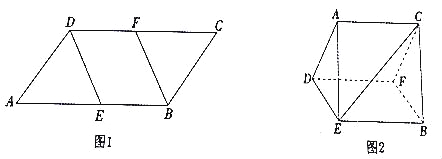
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,分别沿
的中点,分别沿![]() .
.![]() 将
将![]() 和
和![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (点
(点![]() 在平面
在平面![]() 的同侧),连接
的同侧),连接![]() ,如图2所示.
,如图2所示.
(1)求证:![]() ;
;
(2)当![]() ,且平面
,且平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() -
-![]() =1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于
=1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于![]() ,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x,y的方程x2+y2﹣4x+4y+m=0表示一个圆.
(1)求实数m的取值范围;
(2)若m=4,过点P(0,2)的直线l与圆相切,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若过点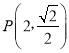 的直线l与椭圆C恒有公共点,求实数a的取值范围;
的直线l与椭圆C恒有公共点,求实数a的取值范围;
(2)若存在以点B(0,2)为圆心的圆与椭圆C有四个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆E的右焦点,直线AF的斜率为2,O为坐标原点.
是椭圆E的右焦点,直线AF的斜率为2,O为坐标原点.
(1)求E的方程;
(2)设过点![]() 且斜率为k的直线
且斜率为k的直线![]() 与椭圆E交于不同的两M、N,且
与椭圆E交于不同的两M、N,且![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高职工的工作积极性,在工资不变的情况下,某企业给职工两种追加奖励性绩效奖金的方案:第一种方案 是每年年末(12月底)追加绩效奖金一次,第一年末追加的绩效奖金为![]() 万元,以后每次所追加的绩效奖金比上次所追加的绩效奖金多
万元,以后每次所追加的绩效奖金比上次所追加的绩效奖金多![]() 万元;第二种方案是每半年(6月底和12月底)各追加绩效奖金一次,第一年的6月底追加的绩效奖金为
万元;第二种方案是每半年(6月底和12月底)各追加绩效奖金一次,第一年的6月底追加的绩效奖金为![]() 万元,以后每次所追加的绩效奖金比上次所追加的绩效奖金多
万元,以后每次所追加的绩效奖金比上次所追加的绩效奖金多![]() 万元.
万元.
假设你准备在该企业工作![]() 年,根据上述方案,试问:
年,根据上述方案,试问:
(1)如果你在该公司只工作2年,你将选择哪一种追加绩效奖金的方案?请说明理由.
(2)如果选择第二种追加绩效奖金的方案比选择第一种方案的奖金总额多,你至少在该企业工作几年?
(3)如果把第二种方案中的每半年追加![]() 万元改成每半年追加
万元改成每半年追加![]() 万元,那么
万元,那么![]() 在什么范围内取值时,选择第二种方案的绩效奖金总额总是比选择第一种方案多?
在什么范围内取值时,选择第二种方案的绩效奖金总额总是比选择第一种方案多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com