
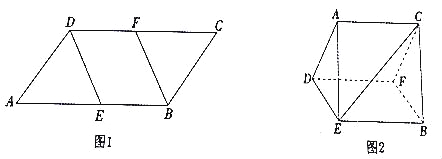
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,分别沿
的中点,分别沿![]() .
.![]() 将
将![]() 和
和![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (点
(点![]() 在平面
在平面![]() 的同侧),连接
的同侧),连接![]() ,如图2所示.
,如图2所示.
(1)求证:![]() ;
;
(2)当![]() ,且平面
,且平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元![]() 今年,工厂第一次投入100万元
今年,工厂第一次投入100万元![]() 科技成本
科技成本![]() ,并计划以后每年比上一年多投入100万元
,并计划以后每年比上一年多投入100万元![]() 科技成本
科技成本![]() ,预计产量年递增10万只,第
,预计产量年递增10万只,第![]() 次投入后,每只产品的固定成本为
次投入后,每只产品的固定成本为![]() 为常数,
为常数,![]() 且
且![]() ,若产品销售价保持不变,第
,若产品销售价保持不变,第![]() 次投入后的年利润为
次投入后的年利润为![]() 万元.
万元.
(1)求![]() 的值,并求出
的值,并求出![]() 的表达式;
的表达式;
(2)问从今年算起第几年利润最高?最高利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足: ![]() ,
, 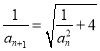 ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,试确定
,试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
(1)命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l为直线,![]() ,
,![]() 为两个不同的平面,若
为两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
(3)给定命题p,q,若“![]() 为真命题”,则
为真命题”,则![]() 是假命题;
是假命题;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于曲线C所在平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线C上的任意两个不同的点A,B恒成立,则称角
对于曲线C上的任意两个不同的点A,B恒成立,则称角![]() 为曲线C相对于点
为曲线C相对于点![]() 的“界角”,并称其中最小的“界角”为曲线C相对于点
的“界角”,并称其中最小的“界角”为曲线C相对于点![]() 的“确界角”.曲线
的“确界角”.曲线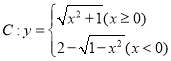 相对于坐标原点
相对于坐标原点![]() 的“确界角”的大小是 _________.
的“确界角”的大小是 _________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .若直线
.若直线![]() 上存在点P,使得
上存在点P,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com