
设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)= (an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′
(an-an+1+an+2)x+an+1·cosx-an+2·sin x满足f′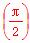 =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2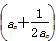 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
定义a*b是向量a和b的“向量积”,它的长度|a*b|=|a||b|sin θ,其中θ为向量a和b的夹角,若u=(2,0),u-v=(1,-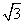 ),则|u*(u+v)|=__
),则|u*(u+v)|=__ ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
将正奇数排列如下表,其中第i行第j个数表示aij(i∈N*,j∈N*),例如a32=9,若aij=2 009,则i+j=________________.
1
3 5
7 9 11
13 15 1 7 19
7 19
…
查看答案和解析>>
科目:高中数学 来源: 题型:
一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第5件工艺品所用的宝石数为______颗;第n件工艺品所用的宝石数为______________颗(结果用n表示).
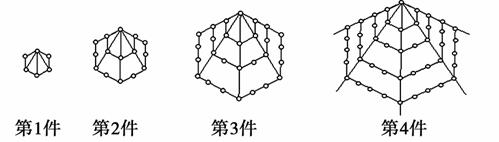
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3-2x2-4x-7,其导函数为f ′(x).则以下四个命题:
①f(x)的单调减区间是(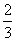 ,2);
,2);
②f(x)的极小值是-15;
③当a>2时,对任意的x>2且x≠a,恒有f(x)>f(a)+f ′(a)(x-a);
④函数f(x)有且只有一个零点.
其中真命题的个数为( )
A.1个 B.2个
C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com