练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】正方体AC1的棱长为1，过点A作平面A1BD的垂线，垂足为点H．有以下四个命题：
    ①点H是△A1BD的垂心；②AH垂直平面CB1D1；
    ③AH= ；④点H到平面A1B1C1D1的距离为 ．
    其中真命题的个数为（ ）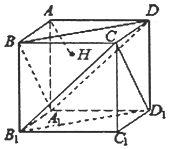

    A.1
    B.2
    C.3
    D.4

    【答案】C
    【解析】解：∵正方体AC1的棱长为1，AH⊥平面A1BD，
    ∴①点H是△A1BD的垂心，正确；
    ②AH垂直平面CB1D1 ， 正确；
    ③AH= AC1= ，正确；
    ④点H到平面A1B1C1D1的距离为 ，错误．
    故选：C．
    【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案，需要熟知两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某班为了提高学生学习英语的兴趣，在班内举行英语写、说、唱综合能力比赛，比赛分为预赛和决赛2个阶段，预赛为笔试，决赛为说英语、唱英语歌曲，将所有参加笔试的同学（成绩得分为整数，满分100分）进行统计，得到频率分布直方图，其中后三个矩形高度之比依次为4:2:1，落在的人数为12人．

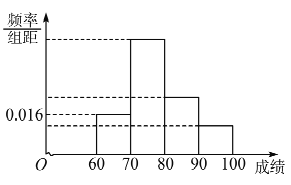
    （Ⅰ）求此班级人数；

    （Ⅱ）按规定预赛成绩不低于90分的选手参加决赛，已知甲乙两位选手已经取得决赛资格，参加决赛的选手按抽签方式决定出场顺序．

    （i）甲不排在第一位乙不排在最后一位的概率；

    （ii）记甲乙二人排在前三位的人数为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间，分别从该品牌手机的甲、乙两种型号中各选取部进行测试，其结果如下：

    甲种手机供电时间（小时）

    乙种手机供电时间（小时）

    （1）求甲、乙两种手机供电时间的平均值与方差，并判断哪种手机电池质量好；

    （2）为了进一步研究乙种手机的电池性能，从上述部乙种手机中随机抽取部，记所抽部手机供电时间不小于小时的个数为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的两个焦点，动点在椭圆上，且使得的点恰有两个，动点到焦点的距离的最大值为.

    （1）求椭圆的方程；

    （2）如图，以椭圆的长轴为直径作圆，过直线上的动点作圆的两条切线，设切点分别为，若直线与椭圆交于不同的两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 在点（1，f（1））处的切线与x轴平行．
    （1）求实数a的值及f（x）的极值；
    （2）若对任意x1 ， x2∈[e2 ， +∞），有| |＞ ，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：空间两向量 =（1，﹣1，m）与 =（1，2，m）的夹角不大于 ；命题q：双曲线 ﹣ =1的离心率e∈（1，2）．若￢q与p∧q均为假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

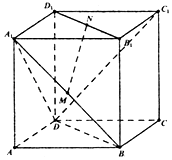
    【题目】如图，在正方体ABCD﹣A1B1C1D1中，点M、N分别是面对角线A1B与B1D1的中点，设 = ， = ， = ．

    （1）以{ ， ， }为基底，表示向量 ；
    （2）求证：MN∥平面BCC1B1；
    （3）求直线MN与平面A1BD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“真人秀”热潮在我国愈演愈烈，为了了解学生是否喜欢某“真人秀”节目，在某中学随机调查了110名学生，得到如下列联表：

    男

    女

    总计

    喜欢

    40

    20

    60

    不喜欢

    20

    30

    50

    总计

    60

    50

    110

    由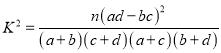算得.

    附表：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是（ ）

    A. 在犯错误的概率不超过的前提下，认为“喜欢该节目与性别有关”

    B. 在犯错误的概率不超过的前提下，认为“喜欢该节目与性别无关”

    C. 有以上的把握认为“喜欢该节目与性别有关”

    D. 有以上的把握认为“喜欢该节目与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行，若集合A={参加北京奥运会比赛的运动员}，集合B={参加北京奥运会比赛的男运动员}．集合C={参加北京奥运会比赛的女运动员}，则下列关系正确的是（　　）
    A.AB
    B.BC
    C.A∩B=C
    D.B∪C=A

    查看答案和解析>>

    同步练习册答案