
设数列 满足前
满足前 项和
项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由于数列的和与通项在一个等式中,通过递推一个式子即可得到关于通项的等式,从而发现是一个等比数列,但一定要验证第一项的结果是否符合;(2)由(1)可得 ,从而
,从而 ,采用分组求和法:
,采用分组求和法: 是等差数列,用等差数列的求和公式进行计算,而
是等差数列,用等差数列的求和公式进行计算,而 是一个等差与一个等比的乘积,故采用错位相减法求和,最后两个和之差即可得到数列
是一个等差与一个等比的乘积,故采用错位相减法求和,最后两个和之差即可得到数列 的前
的前 项和.
项和.
试题解析:(1)当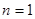 时,
时, ,所以
,所以 1分
1分
当 时,由
时,由 知
知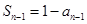
所以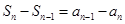 即
即 ,也就是
,也就是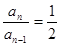 3分
3分
所以数列 的通项公式为
的通项公式为 5分
5分
(2)由(1)可知 ,所以
,所以 6分
6分
则数列 的前
的前 项和
项和
 8分
8分
两式相减,得
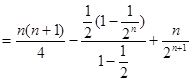 11分
11分
所以数列 的前
的前 项和
项和 12分.
12分.
考点:1.数列的递推思想;2.等比数列的通项公式;3.数列前 项和的计算.
项和的计算.


科目:高中数学 来源: 题型:解答题
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数.
(1)用 表示
表示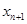 ;
;
(2) ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(3)若数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 项和
项和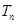 ,求
,求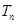 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com