练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

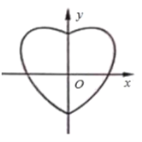
    【题目】数学中有许多形状优美，寓意美好的曲线，曲线C：就是其中之一（如图）.给出下列三个结论：

    ①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；

    ②曲线C上存在到原点的距离超过的点；

    ③曲线C所围成的“心形”区域的面积小于3.其中所有正确结论的个数是（ ）.

    A.0B.1C.2D.3

    【答案】B

    【解析】

    将换成方程不变，所以图形关于轴对称，根据对称性讨论轴右边的图形即可.

    将换成方程不变，所以图形关于轴对称，

    当时，代入可得，，

    即曲线经过，；

    当时，方程变为，

    所以，解得，

    所以只能取整数，

    当时，，解得或，即曲线经过，，

    根据对称性可得曲线经过，，

    故曲线一共经过6个整点，故①正确；

    当时，由可得

    ，（当时取等号），

    ，，

    即曲线C上轴右边的点到原点的距离不超过，

    根据对称性可得：曲线C上任意一点到原点的距离都不超过，故②错误；

    在轴上图形面积大于矩形面积，

    在下方的面积大于等腰三角形的面积，

    因此曲线C所围成的“心形”区域的面积大于，故③错误；

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在新冠病毒疫情爆发期间，口罩成为了个人的必需品.已知某药店有4种不同类型的口罩，，，，其中型口罩仅剩1只（其余3种库存足够）.今甲、乙等5人先后在该药店各购买了1只口罩，统计发现他们恰好购买了3种不同类型的口罩，则所有可能的购买方式共有（ ）

    A.330种B.345种C.360种D.375种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于由正整数构成的数列，若对任意，“且，也是中的项，则称为数列”.设数列|满足，..

    （1）请给出一个的通项公式，使得既是等差数列也是“数列”，并说明理由；

    （2）根据你给出的通项公式，设的前项和为，求满足的正整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（是自然对数的底数）.证明:

    （1）存在唯一的极值点;

    （2）有且仅有两个实根，且两个实根互为相反数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，平面平面，底面为梯形，，.

    （1）平面；

    （2）平面；

    （3）是棱的中点，棱上存在一点，使.

    正确命题的序号为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面直角坐标系xOy中，曲线C的参数方程为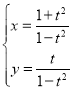（t为参数）.以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（）.

    （1）求曲线C和直线l的直角坐标方程；

    （2）若直线l交曲线C于A，B两点，交x轴于点P，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线：的焦点是椭圆的一个焦点.

    （1）求抛物线的方程；

    （2）设，，为抛物线上的不同三点，点，且.求证：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在我国，大学生就业压力日益严峻，伴随着政府政策引导与社会观念的转变，大学生创业意识，就业方向也悄然发生转变某大学生在国家提供的税收，担保贷款等很多方面的政策扶持下选择加盟某专营店自主

    创业，该专营店统计了近五年来创收利润数（单位：万元）与时间（单位：年）的数据，列表如下：

    1

    2

    3

    4

    5

    2.4

    2.7

    4.1

    6.4

    7.9

    （Ⅰ）依据表中给出的数据，是否可用线性回归模型拟合与的关系，请计算相关系数并加以说明（计算结果精确到0.01）．（若，则线性相关程度很高，可用线性回归模型拟合）：

    （Ⅱ）该专营店为吸引顾客，特推出两种促销方案．

    方案一：每满500元可减50元；

    方案二：每满500元可抽奖一次，每次中奖的概率都为，中奖就可以获得100元现金奖励，假设顾客每次抽奖的结果相互独立．

    ①某位顾客购买了1050元的产品，该顾客选择参加两次抽奖，求该顾客获得100元现金奖励的概率．

    ②某位顾客购买了1500元的产品，作为专营店老板，是希望该顾客直接选择返回150元现金，还是选择参加三次抽奖？说明理由

    附：相关系数公式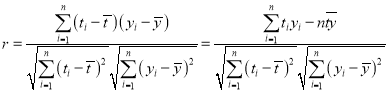

    参考数据：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某小区有一块矩形地块，其中，，单位：百米.已知是一个游泳池，计划在地块内修一条与池边相切于点的直路（宽度不计），交线段于点，交线段于点.现以点为坐标原点，以线段所在直线为轴，建立平面直角坐标系，若池边满足函数的图象，若点到轴距离记为.

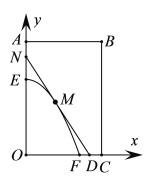
    （1）当时，求直路所在的直线方程；

    （2）当为何值时，地块在直路不含泳池那侧的面积取到最大，最大值时多少？

    查看答案和解析>>

    同步练习册答案