
分析 (1)利用二项展开式的通项公式求出前三项的系数,列出方程求出n,再利用二项展开式的通项公式求出通项,令x的指数为0得到常数项,由方程无解得证;
(2)令展开式中的x的指数为有理数,求出k值,再写出相应的有理项.
解答 解:依题意,前三项系数的绝对值是1,C1n($\frac{1}{2}$),C2n($\frac{1}{2}$)2,
且2C1n•$\frac{1}{2}$=1+C2n($\frac{1}{2}$)2,
即n2-9n+8=0,解得n=8或n=1(不合题意,舍去),
∴展开式的第k+1项为
Ck8($\sqrt{x}$)8-k(-$\frac{1}{2\root{4}{x}}$)k
=(-$\frac{1}{2}$)kCk8•${x}^{\frac{8-k}{2}}$•${x}^{-\frac{k}{4}}$
=(-$\frac{1}{2}$)k•Ck8•${x}^{\frac{16-3k}{4}}$;
(1)证明:若第k+1项为常数项,
当且仅当$\frac{16-3k}{4}$=0,即3k=16,
由k∈Z得这是不可能的,
所以其展开式中没有常数项;
(2)若第k+1项为有理项,当且仅当$\frac{16-3k}{4}$为整数,
∵0≤k≤8,k∈Z,∴k=0,4,8,
即展开式中的有理项共有三项,它们是:
T1=x4,T5=$\frac{35}{8}$x,T9=$\frac{1}{256}$x-2.
点评 本题考查了利用二项展开式的通项公式解决二项展开式的特定项问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
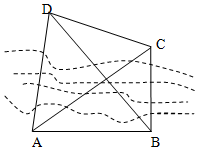 如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.
如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | $3+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 70 | 40 |
| 不需要 | 30 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com