
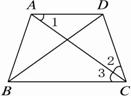
已知:在梯形ABCD中(如上图),AB=DC=AD,AC和BD是它的对角线.求证:AC平分∠BCD,DB平分∠CBA.
证明:(1)等腰三角形两底角相等(大前提),?
△DAC是等腰三角形,DA、DC是两腰(小前提),?
∠1=∠2(结论).?
(2)两条平行线被第三条直线截出的内错角相等(大前提),?
∠1和∠3是平行线AD、BC被AC截出的内错角(小前提),?
∠1=∠3(结论).?
(3)等于同一个量的两个量相等(大前提),?
∠2和∠3都等于∠1(小前提),?
∠2=∠3(结论),即AC平分∠BCD.?
(4)同理,DB平分∠CBA.?
温馨提示:这个证明中如果把(4)也详细地写出,则一共通过六次三段论的形式.因此一个命题的证明形式,确切地常叫做复合三段论的形式,或说命题的推证方法是复合三段论法,但是事实上,每一次三段论的大前提并不写出,某一次三段论的小前提如果是它前面某次三段论的结论,也就不再写出了.如例3的证明可写成:?
∵DA=DC(省略了大前提),?
∴∠1=∠2.?
∵AD∥BC,且被AC截得的内错角为∠1和∠3(省略大前提),?
∴∠1=∠3.?
∴∠2=∠3,即AC平分∠BCD(省略大前提,小前提).?
同理可证DB平分∠ABC.?
这样,一般地在推论命题时所采用的这种表达的方法,就叫做简化的复合三段论法.


科目:高中数学 来源:同步题 题型:证明题
查看答案和解析>>
科目:高中数学 来源: 题型:
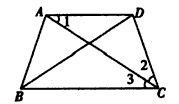
已知在梯形ABCD中(如图2-1-11),AB=DC=AD,AC和BD是它的对角线,求证:AC平分∠BCD,DB平分∠CBA.

图2-1-11
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在梯形ABCD中(如图2-1-11),AB=DC=AD,AC和BD是它的对角线,求证:AC平分∠BCD,DB平分∠CBA.
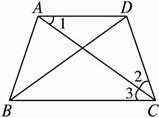
图2-1-11
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在如图所示的梯形ABCD中,AD∥BC,AD=DC=AD,AC和BD是它的对角线.
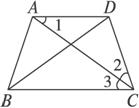
求证:AC平分∠BCD,BD平分∠CBA.
分析:本题可由三段论逐步推理论证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com