
分析 (1)求出函数的导数,得到关于a,b的方程组,解出即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值点即可.
解答 解:(1)f′(x)=3x2-3a,
∵曲线y=f(x)在点(2,f(x))处与直线y=8相切,
∴$\left\{\begin{array}{l}{f′(2)=0}\\{f(2)=8}\end{array}\right.$,即$\left\{\begin{array}{l}{3(4-a)=0}\\{8-6a+b=8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=4}\\{b=24}\end{array}\right.$;
(2)∵f′(x)=3(x2-a),(a≠0),
当a<0时,f′(x)>0,f(x)在R上单调递增,
此时函数f(x)没有极值点.
当a>0时,由f′(x)=0,解得:x=±$\sqrt{a}$,
当x∈(-∞,-$\sqrt{a}$)时,f′(x)>0,函数f(x)单调递增,
当x∈(-$\sqrt{a}$,$\sqrt{a}$)时,f′(x)<0,函数f(x)单调递减,
当x∈[$\sqrt{a}$,+∞)时,f′(x)>0,函数f(x)单调递增,
∴此时x=-$\sqrt{a}$是f(x)的极大值点,x=$\sqrt{a}$是f(x)的极小值点.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:“若x2-3x+2=0,则x=2”的否命题为假命题 | |
| B. | 命题”存在x≥0,使2x=5”的否定为”对任意x<0,都有2x≠5” | |
| C. | 若p且q为假命题,则p、q均为假命题 | |
| D. | “a=0”是“复数a+bi(a,b∈R)为纯虚数”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知圆锥OO1和圆柱O1O2的组合体(它们的底面重合),圆锥的底面圆O1半径为r=5,OA为圆锥的母线,AB为圆柱O1O2的母线,D、E为下底面圆O2上的两点,且DE=6,AB=6.4,AO=5$\sqrt{2}$,AO⊥AD.
如图,已知圆锥OO1和圆柱O1O2的组合体(它们的底面重合),圆锥的底面圆O1半径为r=5,OA为圆锥的母线,AB为圆柱O1O2的母线,D、E为下底面圆O2上的两点,且DE=6,AB=6.4,AO=5$\sqrt{2}$,AO⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
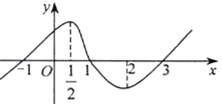 已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).
已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com