C
分析:对f(x)求导数,得f'(x)=1-6xcosx
2.通过特殊值代入,结合函数图象观察可得f(x)在(0,π)上共有5个单调区间.再用零点存在性质定理加以验证,可得函数f(x)在(0,π)上有4个零点,而在(π,+∞)上没有零点.结合f(0)=0可得f(x)在[0,+∞)上总共5个零点.
解答:∵函数解析式为f(x)=x-3sinx
2,

∴f'(x)=1-3(cosx
2)•2x=1-6xcosx
2.
可得f'(0)=1>0,f'(

)=1-

<0,f'(

)=1>0,
f'(
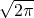
)=1-6
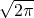
<0,f'(

)=1+6

>0,
因此,f'(x)在区间(0,

),(

,

),(

,
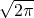
),(
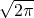
,

)上分别有一个零点
将这些零点分别设为x
1、x
2、x
3、x
4,
可得函数f(x)=x-3sinx
2在区间(0,x
1),(x
2,x
3),(x
4,π)上
是增函数;在区间(x
1,x
2),(x
3,x
4)上是减函数.
即f(x)在(0,π)上共有5个单调区间
∵f(0.1)>0,f(

)=

-3<0,f(
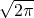
)=
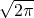
>0,
f(

)=

-3<0,f(

)=

>0
∴f(x)在(0.1,

)、(

,
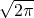
)、(
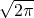
,

)、(

,

)上各有一个零点
而f(0)=0,且x>π时f(x)=x-3sinx
2>π-3>0
∴f(x)在[0,π]上有5个零点,而在(π,+∞)上没有零点.因此函数f(x)在[0,+∞)上总共5个零点.
故选:C
点评:本题给出函数f(x)=x-3sinx
2,求它在[0,+∞)上的零点个数.着重考查了利用导数研究函数的单调性和零点存在性定理等知识,属于中档题.


 )=1-
)=1- <0,f'(
<0,f'( )=1>0,
)=1>0,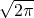 )=1-6
)=1-6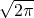 <0,f'(
<0,f'( )=1+6
)=1+6 >0,
>0, ),(
),( ,
, ),(
),( ,
,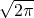 ),(
),(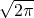 ,
, )上分别有一个零点
)上分别有一个零点 )=
)= -3<0,f(
-3<0,f(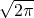 )=
)=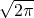 >0,
>0, )=
)= -3<0,f(
-3<0,f( )=
)= >0
>0 )、(
)、( ,
,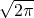 )、(
)、(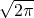 ,
, )、(
)、( ,
, )上各有一个零点
)上各有一个零点

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<