
设![]() 为非负实数,函数
为非负实数,函数![]() .
.
(Ⅰ)当![]() 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数![]() 的零点个数,并求出零点.(Ⅲ)当
的零点个数,并求出零点.(Ⅲ)当![]() 时,
时,![]() ,试求
,试求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时
取得最大值时![]() 的表达式。
的表达式。
解析:(Ⅰ)当![]() 时,
时,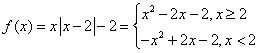 , -------------1分
, -------------1分
① 当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增; --------------2分
上单调递增; --------------2分
② 当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增; --------------3分
上单调递增; --------------3分
综上所述,![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() 。------4分
。------4分
(Ⅱ)(1)当![]() 时,
时,![]() ,函数
,函数![]() 的零点为
的零点为![]() ; -----5分
; -----5分
(2)当![]() 时,
时,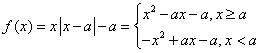 , --------------6分
, --------------6分
故当![]() 时,
时,![]() ,二次函数对称轴
,二次函数对称轴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() ; -----------7分
; -----------7分
当![]() 时,
时,![]() ,二次函数对称轴
,二次函数对称轴![]() ,
,![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增; ------------------------------8分
上单调递增; ------------------------------8分
∴![]() 的极大值为
的极大值为![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 与
与![]() 轴只有唯一交点,即唯一零点,
轴只有唯一交点,即唯一零点,
由![]() 解之得
解之得
函数![]() 的零点为
的零点为![]() 或
或![]() (舍去);
(舍去);
----------------------10分
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 与
与![]() 轴有两个交点,即两个零点,分别为
轴有两个交点,即两个零点,分别为![]()
和![]() ; -----------------------11分
; -----------------------11分
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 与
与![]() 轴有三个交点,即有三个零点,
轴有三个交点,即有三个零点,
由![]() 解得,
解得,![]() ,
,
∴函数![]() 的零点为
的零点为![]() 和
和![]() 。-----------12分
。-----------12分
综上可得,当![]() 时,函数的零点为
时,函数的零点为![]() ;
;
当![]() 时,函数有一个零点,且零点为
时,函数有一个零点,且零点为![]() ;
;
当![]() 时,有两个零点
时,有两个零点![]() 和
和![]() ;
;
当![]() 时,函数有三个零点
时,函数有三个零点![]() 和
和


科目:高中数学 来源: 题型:
(本小题满分14分) 设![]() 为非负实数,函数
为非负实数,函数![]() .
.
(Ⅰ)当![]() 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数![]() 的零点个数,并求出零点.(Ⅲ)当
的零点个数,并求出零点.(Ⅲ)当![]() 时,
时,![]() ,试求
,试求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时
取得最大值时![]() 的表达式。
的表达式。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分) 设![]() 为非负实数,函数
为非负实数,函数![]() .
.
(Ⅰ)当![]() 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数![]() 的零点个数,并求出零点.(Ⅲ)当
的零点个数,并求出零点.(Ⅲ)当![]() 时,
时,![]() ,试求
,试求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时
取得最大值时![]() 的表达式。
的表达式。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东高一第二次月考数学试卷(解析版) 题型:解答题
(本题满分14分)设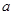 为非负实数,函数
为非负实数,函数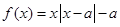 .
.
(Ⅰ)当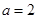 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数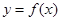 的零点个数,并求出零点.
的零点个数,并求出零点.
查看答案和解析>>
科目:高中数学 来源:2015届江西省高一第二次月考数学试卷(解析版) 题型:解答题
(本题满分14分)设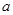 为非负实数,函数
为非负实数,函数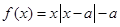 .
.
(Ⅰ)当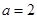 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数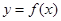 的零点个数.
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com