
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() (其中
(其中![]() ,
,![]() 是自然对数的底数)上的最小值;
是自然对数的底数)上的最小值;
(2)若存在与函数![]() ,
,![]() 的图象都相切的直线,求实数
的图象都相切的直线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据题意得![]() ,利用导数,分类讨论求得函数
,利用导数,分类讨论求得函数![]() 的单调性,即可求解函数的最小值;
的单调性,即可求解函数的最小值;
(2)设函数![]() 在点
在点![]() 处与函数
处与函数![]() 在点
在点![]() 处有相同的切线,分别求得
处有相同的切线,分别求得![]() ,利用斜率相等,转化为方程
,利用斜率相等,转化为方程![]() 有解,设函数
有解,设函数![]() ,利用导数求得函数的单调性和最值,即可求解。
,利用导数求得函数的单调性和最值,即可求解。
(1)由题意,可得![]() ,
,
![]()
![]() ,
,
令![]() ,得
,得![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
②当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() .
.
综上,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
(2)设函数![]() 在点
在点![]() 处与函数
处与函数![]() 在点
在点![]() 处有相同的切线,
处有相同的切线,
则![]() ,∴
,∴![]() ,
,
∴![]() ,代入
,代入![]()
得![]() .
.
∴问题转化为:关于![]() 的方程
的方程![]() 有解,
有解,
设![]() ,则函数
,则函数![]() 有零点,
有零点,
∵![]() ,当
,当![]() 时,
时,![]() ,∴
,∴![]() .
.
∴问题转化为:![]() 的最小值小于或等于0.
的最小值小于或等于0.
![]() ,
,
设![]() ,则
,则
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 的最小值为
的最小值为![]() .
.
由![]() 知
知![]() ,故
,故![]() .
.
设![]() ,
,
则![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴当
,∴当![]() 时,
时,![]() ,
,
∴![]() 的最小值
的最小值![]() 等价于
等价于![]() .
.
又∵函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() .
.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 满足
满足![]() 且
且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 边上的动点,且
边上的动点,且![]() .
.
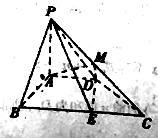
(1)求证:平面![]() 平面
平面![]() ;
;
(2)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,试求出实数
?若存在,试求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2-(3+a)x+3a<0,其中a<3;q:x2+4x-5>0.
(1)若p是q的必要不充分条件,求实数a的取值范围;
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解居民参加体育锻炼情况,随机抽取18名男性居民,12名女性居民对他们参加体育锻炼的情况进行问卷调查.现按参加体育锻炼的情况将居民分成3类:甲类(不参加体育锻炼),乙类(参加体育锻炼,但平均每周参加体育锻炼的时间不超过5个小时),丙类(参加体育锻炼,且平均每周参加体育锻炼的时间超过5个小时),调查结果如下表:
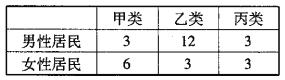
(1)根据表中的统计数据,完成下面列联表,并判断是否有![]() 的把握认为参加体育锻炼与性别有关?
的把握认为参加体育锻炼与性别有关?
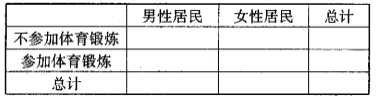
(2)从抽出的女性居民中再随机抽取3人进一步了解情况,记![]() 为抽取的这3名女性居民中甲类和丙类人数差的绝对值,求
为抽取的这3名女性居民中甲类和丙类人数差的绝对值,求![]() 的数学期望.
的数学期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
A. 众数 B. 平均数 C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为( )
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A. ![]() 天B.
天B. ![]() 天C.
天C. ![]() 天D.
天D. ![]() 天
天
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com