
已知向量 ,
, ,设函数
,设函数 ,
, .
.
(Ⅰ)求 的最小正周期与最大值;
的最小正周期与最大值;
(Ⅱ)在 中,
中,
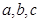 分别是角
分别是角 的对边,若
的对边,若 的面积为
的面积为 ,求
,求 的值.
的值.
(Ⅰ) 的最小正周期为
的最小正周期为 ,
, 的最大值为5;(Ⅱ)
的最大值为5;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)求 的最小正周期与最大值,首先须求出
的最小正周期与最大值,首先须求出 的解析式,由已知向量
的解析式,由已知向量 ,
, ,函数
,函数 ,可将
,可将 代入,根据数量积求得
代入,根据数量积求得
 ,进行三角恒等变化,像这一类题,求周期与最大值问题,常常采用把它化成一个角的一个三角函数,即化成
,进行三角恒等变化,像这一类题,求周期与最大值问题,常常采用把它化成一个角的一个三角函数,即化成 ,利用它的图象与性质,,求出周期与最大值,本题利用两角和与差的三角函数公式整理成
,利用它的图象与性质,,求出周期与最大值,本题利用两角和与差的三角函数公式整理成 ,从而求得
,从而求得 的最小正周期与最大值;(Ⅱ)在
的最小正周期与最大值;(Ⅱ)在 中,
中,
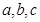 分别是角
分别是角 的对边,若
的对边,若 的面积为
的面积为 ,求
,求 的值,要求
的值,要求 的值,一般用正弦定理或余弦定理,本题注意到
的值,一般用正弦定理或余弦定理,本题注意到 ,由
,由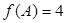 得,可求出角A的值,由已知
得,可求出角A的值,由已知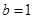 ,
, 的面积为
的面积为 ,可利用面积公式
,可利用面积公式 ,求出
,求出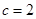 ,已知两边及夹角,可利用余弦定理求出
,已知两边及夹角,可利用余弦定理求出 ,解此类题,主要分清边角关系即可,一般不难.
,解此类题,主要分清边角关系即可,一般不难.
试题解析:(Ⅰ)
 ,∴
,∴
 的最小正周期为
的最小正周期为 ,
, 的最大值为5.
的最大值为5.
(Ⅱ)由 得,
得,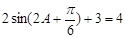 ,即
,即
 ,∵
,∵
 , ∴
, ∴ ,
,
∴  ,又
,又 , 即
, 即 , ∴
, ∴
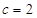 ,由余弦定理得,
,由余弦定理得, ,∴
,∴ 
考点:两角和正弦公式,正弦函数的周期性与最值,根据三角函数的值求角,解三角形,考查学生的基本运算能力.


科目:高中数学 来源:2012-2013学年山东省威海市乳山一中高三(上)12月月考数学试卷(文科)(解析版) 题型:解答题
 ,
, ,设函数
,设函数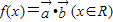 的图象关于直线
的图象关于直线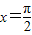 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省青岛市黄岛开发区一中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
 ,
, ,设函数
,设函数 •
• ,若函数g(x)的图象与f(x)的图象关于坐标原点对称.
,若函数g(x)的图象与f(x)的图象关于坐标原点对称. ]上的最大值,并求出此时x的值;
]上的最大值,并求出此时x的值; ,b+c=7,△ABC的面积为2
,b+c=7,△ABC的面积为2 ,求边a的长.
,求边a的长.查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市潼南县古溪中学高三(上)第二次月考数学试卷(解析版) 题型:解答题
 ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域.查看答案和解析>>
科目:高中数学 来源:2012年辽宁省沈阳市高考数学二模试卷(文科)(解析版) 题型:解答题
 ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三第七次模拟考试文科数学试卷(解析版) 题型:解答题
已知向量 ,
, ,设函数
,设函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)在 中,若
中,若 的面积为
的面积为 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com