
试比较2n+2与n2的大小(n∈N*),并用数学归纳法证明你的结论.
当n=1时,21+2=4>n2=1;
当n=2时,22+2=6>n2=4;
当n=3时,23+2=10>n2=9;
当n=4时,24+2=18>n2=16.
由此可以猜想,2n+2>n2(n∈N*)成立.
下面用数学归纳法证明:
(1) 当n=1时,左边=21+2=4,右边=1,左边>右边,所以原不等式成立;
当n=2时,左边=22+2=6,
右边=22=4,左边>右边;
当n=3时,左边=23+2=10,右边=32=9,左边>右边.
(2) 假设n=k(k≥3且k∈N*)时,不等式成立,
即2k+2>k2.那么当n=k+1时,
2k+1+2=2·2k+2=2(2k+2)-2>2·k2-2.
又因为2k2-2-(k+1)2=k2-2k-3=(k-3)(k+1)≥0,
即2k2-2≥(k+1)2,故2k+1+2>(k+1)2成立.
根据(1)和(2),可知原不等式对于任何n∈N*都成立.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
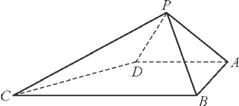
如图,在四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.
(1) 求证:PB⊥CD;
(2) 求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
在等比数列{an}中,an>0(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.
(1) 求数列{an}的通项公式;
(2) 设bn=log2an,求数列{bn}的前n项和Sn;
(3) 是否存在k∈N*,使得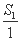 +
+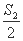 +…+
+…+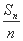 <k对任意n∈N*恒成立?若存在,求出k的最小值;若不存在,请说明理由.
<k对任意n∈N*恒成立?若存在,求出k的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com