
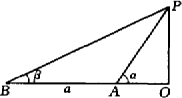
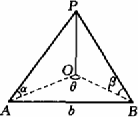
为了测量某一电视塔的高度,同学们采用了如图所示的两种方法,请依据所给条件,求出塔高.
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:044
如图,为了测量建造中的某城市电视塔已达的高度,小明在学校操场上的某一直线上选A、B、C三点,且AB=BC=60 m.分别在A、B、C三点观察塔的最高点,测得倾角为45°,54.2°,60°,小明身高为1.5 m,试求建造中的电视塔现在已达的高度(结果保留一位小数).

查看答案和解析>>
科目:高中数学 来源: 题型:
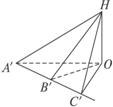
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com