
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
分析 由$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$,展开后代入已知条件得答案.
解答 解:∵$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$,且$|{\overrightarrow a}|=1$,$|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$,
∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}=|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}+2|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{3}=7$,
即1+$|\overrightarrow{b}{|}^{2}+2×1×\frac{1}{2}|\overrightarrow{b}|=7$,
∴$|\overrightarrow{b}{|}^{2}+|\overrightarrow{b}|-6=0$,解得:$|\overrightarrow{b}|=-3$(舍)或$|{\overrightarrow b}|$=2.
故选:A.
点评 本题考查平面向量的数量积运算,关键是明确${\overrightarrow{a}}^{2}=|\overrightarrow{a}{|}^{2}$,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
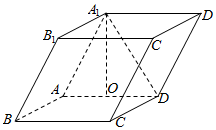 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,且AD=2CD=2,AA1=2,$∠{A_1}AD=\frac{π}{3}$,若O为AD的中点,且CD⊥A1O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
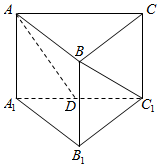 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{{\sqrt{7}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
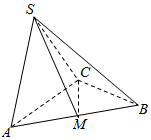 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x<-1} | D. | {x|-1≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com