
分析 (1)设动点M的坐标为(x,y),根据两点的距离公式结合题意建立关于x、y的等式,化简整理得到x2=4y(y≤4)或x2=-16(y-5)(y>4),从而得到轨迹是由两个抛物线弧连接而成,其图形如图所示;
(2)根据轨迹E的形状,直线l:y=x+m分别将与抛物线段联解,得到直线l与轨迹E有唯一公共点的两个界点处m的值,再将直线l平移进行观察,即可得到实数m的取值范围;将两个抛物线段E1与E2的方程与直线l方程联解,可得交点A.B的横坐标关于m的式子,运用两点间的距离公式算出|AB|,运用导数研究$f(m)=\sqrt{1+m}+2\sqrt{9-m}(0<m<8)$的单调性,即可得到当m=1时,|AB|的最大值.
解答 解:(1)设M(x,y),由题设知:$\sqrt{{x^2}+{{(y-1)}^2}}+|{y-4}|=5$,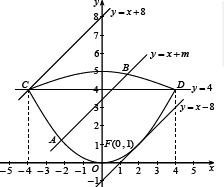
①当y≥4时,x2=-16(y-5)即$y=-\frac{x^2}{16}+5(-4≤x≤4)$,其轨迹为E2,
②当y<4时,x2=4y即$y=\frac{1}{4}{x^2}(-4≤x≤4)$,其轨迹为E1,①和②均为E的轨迹方程.
(2)由$\left\{{\begin{array}{l}{y=-\frac{x^2}{16}+5}\\{y=\frac{x^2}{4}}\end{array}}\right.$解得C(-4,4),D(4,4),
当l过点C时,m=8,
当l与$y=\frac{1}{4}{x^2}$相切于P(x0,y0)时,$y'=\frac{x}{2}$,∴$\frac{x_0}{2}=1$,解得x0=2,y0=1,∴切点P(2,1),∴m=-1.
综上:m∈(-1,8)…(8分)
(3)①当-1<m≤0时,l与E的两个交点均在E1上.∴$0<|{AB}|≤|{OD}|=4\sqrt{2}$.
②当0<m<8时,l与E的两个交点A在E1上,B在E2上,
由$\left\{{\begin{array}{l}{y=x+m}\\{y=\frac{x^2}{4}}\end{array}}\right.$解得:$x=2±2\sqrt{1+m}$,∴${x_A}=2-2\sqrt{1+m}$,
由$\left\{{\begin{array}{l}{y=x+m}\\{y=-\frac{x^2}{16}+5}\end{array}}\right.$解得:$x=-8±4\sqrt{9-m}$,∴${x_B}=-8+4\sqrt{9-m}$,
∴$|{AB}|=\sqrt{{{({x_A}-{x_B})}^2}+{{({y_A}-{y_B})}^2}}=\sqrt{2}|{{x_B}-{x_A}}|=2\sqrt{2}(\sqrt{1+m}+2\sqrt{9-m}-5)$
令$f(m)=\sqrt{1+m}+2\sqrt{9-m}(0<m<8)$.
∴$f'(m)=\frac{1}{{2\sqrt{1+m}}}-\frac{1}{{\sqrt{9-m}}}=\frac{{\sqrt{9-m}-2\sqrt{1+m}}}{{2\sqrt{1+m}•\sqrt{9-m}}}$=$\frac{5(1-m)}{{2\sqrt{1+m}•\sqrt{9-m}(\sqrt{9-m}+2\sqrt{1+m})}}$
令f'(m)=0,解得m=1,
∴当m∈(0,1),f'(m)>0,m∈(1,8),f'(m)<0,
∵$f{(m)_{max}}=f(1)=5\sqrt{2}$,∴${|{AB}|_{max}}=20-10\sqrt{2}>4\sqrt{2}$,
综上:${|{AB}|_{max}}=20-10\sqrt{2}$…(12分)
点评 本题给出动点M满足的条件,求M的轨迹方程,并讨论了直线l与M的轨迹相交截得弦AB长度最大值.着重考查了抛物线的简单几何性质、直线与抛物线的位置关系、利用导数研究函数的单调性和轨迹方程的讨论等知识,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{14}}{14}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | $\frac{2015}{2}$ | C. | 2014 | D. | 1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
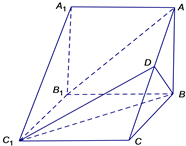 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com