函数f(x)=x2-2ax+1,(a∈R),g(x)=x-1同时符合以下条件:
(1)任x∈R,f(x)或g(x)非负;
(2)存在x∈R,f(x)•g(x)>0;
则实数α的范围是( )
A.(0,2)
B.[0,1]
C.(-1,2)
D.[-1,1]
【答案】
分析:由g(x)=x-1,知当x<1 时,g(x)<0;当x>1时,g(x)>0.由x<1时,f(x)=x
2-2ax+1=(x-a)
2+1-a
2≥0,能求出实数α的范围.
解答:解:∵g(x)=x-1,
∴当x<1 时,g(x)<0;当x>1时,g(x)>0.
∵任x∈R,f(x)或g(x)非负,
∴x<1时,f(x)=x
2-2ax+1=(x-a)
2+1-a
2≥0,
①若1-a
2≥0 即-1≤a≤1时,则f(x)在R上非负,成立;
②若1-a
2<0,即a<-1或a>1时,解得a-
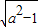
>1,即a<1.
又∵x充分大时,f(x)>0,g(x)>0
∴存在x∈R,f(x)•g(x)>0.
综上,实数α的范围是[-1,1].
故选D.
点评:本题考查二次函数的性质和应用,解题时要认真审题,注意等价转化思想的合理运用.

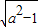 >1,即a<1.
>1,即a<1.
