
已知函数 (其中
(其中 为常数).
为常数).
(Ⅰ)当 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)当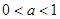 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且 .证明:
.证明: .
.
(Ⅰ)单调减区间为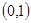 ,
,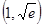 ;增区间为
;增区间为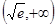 .(Ⅱ)详见解析.
.(Ⅱ)详见解析.
解析试题分析:(Ⅰ)将
科目:高中数学
来源:
题型:解答题
设函数f(x)=
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
设二次函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 代入
代入 ,然后求导便可得其单调区间.
,然后求导便可得其单调区间.
(Ⅱ)我们分以下几步来分析.
第一步、对 求导得:
求导得: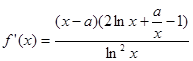 .显然
.显然 是它的一个极值点,下面我们要弄清楚
是它的一个极值点,下面我们要弄清楚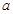 应该是
应该是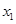 还是
还是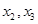 .另两个极值点便是方程
.另两个极值点便是方程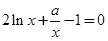 的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数
的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数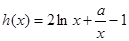 .
.
第二步、对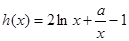 求导得:
求导得: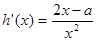
∴函数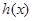 在
在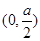 上单调递减,在
上单调递减,在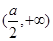 上单调递增
上单调递增
当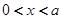 时,
时,
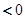 ,
,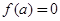 .又
.又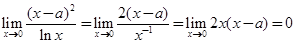 ,
,
所以 在
在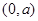 上必有一个极值点.
上必有一个极值点.
因为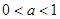 ,所以
,所以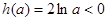 ,
,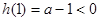 ,
,
∴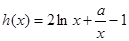 的两个零点必有一个小于
的两个零点必有一个小于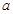 (实际上比
(实际上比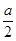 还小),而另一个大于1,
还小),而另一个大于1,
∴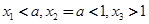 .
.
∴当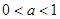 时,
时,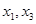 是函数
是函数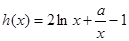 的两个零点,且
的两个零点,且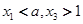 .
.
即有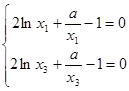 .这样问题转化为在该条件下证明
.这样问题转化为在该条件下证明 .那么这个不等式如何证呢?
.那么这个不等式如何证呢?
第三步、注意到待证不等式 中不含
中不含 ,故考虑消去
,故考虑消去 ,找到
,找到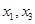 之间的关系式.
之间的关系式.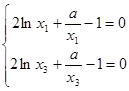 消去
消去 有
有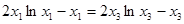 .
.
令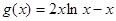 ,
,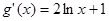 有零点
有零点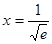 .
.
∴函数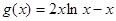 在
在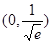 上递减,在
上递减,在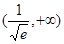 上递增,
上递增,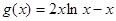 在
在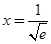 处取得极小值.由于
处取得极小值.由于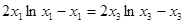 ,所以
,所以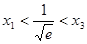 .
.
因为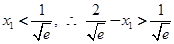 .
.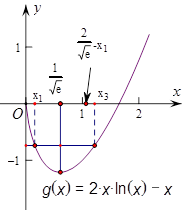
所以要证明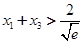 ,只需证
,只需证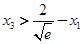 .那么这个不等式又如何证明呢?
.那么这个不等式又如何证明呢?
因为函数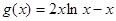 在
在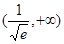 上递增,所以转化为证
上递增,所以转化为证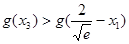 .
. 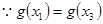
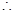 即证
即证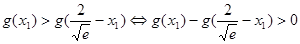 .
.
这个不等式,通过构造函数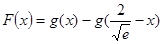 ,再利用导数就很容易证明了.
,再利用导数就很容易证明了.
试题解析:(Ⅰ)求导得: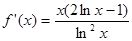 .
.
令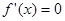 可得
可得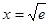 .列表如下:
.列表如下:

小卷实战系列答案

本土教辅名校学案初中生辅导系列答案
轻巧夺冠青岛专用系列答案
名题文化步步高书系名题系列答案
倍速训练法一练通系列答案
金牌教辅夺冠金卷系列答案
海淀名师名校百分卷系列答案
8848高中同步学情跟进卷系列答案
中考实战名校在招手系列答案
 +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数)
(1)求y=f(x)-g(x)(x>0)的最小值;
(2)是否存在一次函数h(x)=kx+b使得f(x)≥h(x)且h(x)≥g(x)对一切x>0恒成立;若存在,求出一次函数的表达式,若不存在,说明理由:
3)数列{ }中,a1=1,
}中,a1=1, =g(
=g(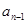 )(n≥2),求证:
)(n≥2),求证: <
<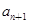 <
< <1且
<1且 <
< .
. ,(
,( 且
且 ).
).
(1)设 ,令
,令 ,试判断函数
,试判断函数 在
在 上的单调性并证明你的结论;
上的单调性并证明你的结论;
(2)若 且
且
 的定义域和值域都是
的定义域和值域都是 ,求
,求 的最大值;
的最大值;
(3)若不等式 对
对 恒成立,求实数
恒成立,求实数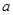 的取值范围;
的取值范围; 的图像过原点,
的图像过原点, ,
, 的导函数为
的导函数为 ,且
,且 ,
,

(1)求函数 ,
, 的解析式;
的解析式;
(2)求 的极小值;
的极小值;
(3)是否存在实常数 和
和 ,使得
,使得 和
和 若存在,求出
若存在,求出 和
和 的值;若不存在,说明理由.
的值;若不存在,说明理由.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号