
在等比数列{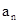 }中,如果
}中,如果 。
。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
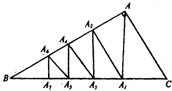 如图,在Rt△ABC中,∠BAC=90°,作AA1⊥BC,A1A2⊥AB,A2A3⊥BC,A3A4⊥AB,A4A5⊥BC,A5A6⊥AB,A6A7⊥BC,A1,A2,A3,A4,A5,A6,A7分别为垂足:
如图,在Rt△ABC中,∠BAC=90°,作AA1⊥BC,A1A2⊥AB,A2A3⊥BC,A3A4⊥AB,A4A5⊥BC,A5A6⊥AB,A6A7⊥BC,A1,A2,A3,A4,A5,A6,A7分别为垂足:查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•焦作模拟)在公比为2的等比数列{an}中,a2与a4的等差中项是5
(2012•焦作模拟)在公比为2的等比数列{an}中,a2与a4的等差中项是5| 3 |
| π |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.
(1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
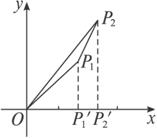
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2012年河南省焦作市高三第一次质量检测数学试卷(理科)(解析版) 题型:解答题
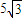 .
. ),|ϕ|<π的一部分图象如图所示,M(-1,|a1|),
),|ϕ|<π的一部分图象如图所示,M(-1,|a1|), 为图象上的两点,设∠MPN=β,其中P与坐标原因O重合,0≤β≤π,求tan(φ-β)的值.
为图象上的两点,设∠MPN=β,其中P与坐标原因O重合,0≤β≤π,求tan(φ-β)的值.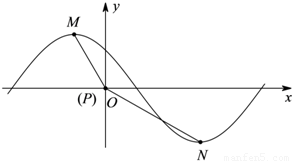
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com