练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，四棱柱中, 侧棱底面，，，，为棱的中点.

    (1) 证明：；

    (2) 设点在线段上, 且直线与平面所成角的正弦值为, 求线段的长.

     

    （1）证明见解析；（2）．

    【解析】

    试题分析：

    解题思路：根据题意建立空间直角坐标系，写点的坐标与有关向量，利用直线的方向向量的数量积为0证明两直线垂直；利用线面角的公式列出关于的方程即可.

    规律总结：证明平行或垂直问题，一般有两个思路:①利用一个判定与性质进行证明；②转化为空间向量的平行与垂直进行证明；求角或距离问题，往往利用空间向量进行求解.

    试题解析：以点为原点建立空间直角坐标系，依题意得，

    证明：，于是，所以；

    【解析】
    设有

    .可取为平面的一个法向量.

    设为直线与平面所成角，则

    于是解得所以.

    考点：1.直线的垂直关系的证明；2.直线与平面所成的角的求法.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届云南省高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    函数处的切线方程是( )

    A． B．

    C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届云南省云龙县高二下学期期末考试试卷理科数学试卷（解析版） 题型：选择题

    设直线和平面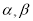,下列四个命题中，正确的是（ ）

    A.若，则

    B.，则

    C.若，则

    D.，则

     

    查看答案和解析>>

    科目：高中数学 来源：2015届云南省云龙县高二下学期期末考试试卷文科数学试卷（解析版） 题型：选择题

    下列命题中，真命题的是 （ ）

    A.已知则的最小值是

    B.已知数列的通项公式为，则的最小项为

    C.已知实数满足，则的最大值是

    D.已知实数满足，则的最小值是

     

    查看答案和解析>>

    科目：高中数学 来源：2015届云南省云龙县高二下学期期末考试试卷文科数学试卷（解析版） 题型：选择题

    直线与直线垂直，则 （ ）

    A. B. C. D.不存在

     

    查看答案和解析>>

    科目：高中数学 来源：2015届上海市高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    使得的展开式中含有常数项的最小的为（　　）

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届上海市高二下学期期末考试理科数学试卷（解析版） 题型：填空题

    在长方体中，已知，为的中点，则直线与平面的距离是___________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届上海市高二下学期期末考试文科数学试卷（解析版） 题型：选择题

    某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70), [70,80), [80,90), [90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为（　　）

    A．588 B．480 C．450 D．120

     

    查看答案和解析>>

    科目：高中数学 来源：2015届上海市高二下学期期中数学试卷（解析版） 题型：解答题

    已知：对于任意的多项式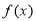与任意复数z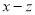，整除。利用上述定理解决下列问题：

    在复数范围内分解因式：；

    求所有满足整除的正整数n构成的集合A。

     

    查看答案和解析>>

    同步练习册答案