练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，底面，，为等边三角形，，，为的中点.

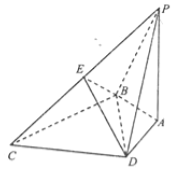
    （1）求；

    （2）求平面与平面所成二面角的正弦值.

    【答案】（1）；（2）.

    【解析】

    试题分析：（1）连接，因为底面，，所以，所以平面.所以，因为为等边三角形，所以.又已知，，可得；（2）分别以所在直线为轴，过且平行的直线为轴建立空间直角坐标系，计算得平面的法向量为,平面的法向量为，所以.

    试题解析：

    （1）连接，因为底面，平面，所以.

    又因为，，所以平面.

    因为平面，所以.因为为等边三角形，所以.

    又已知，，可得.

    （2）分别以所在直线为轴，过且平行的直线为轴建立空间直角坐标系，

    .

    由题意可知平面的法向量为.

    设平面的法向量为，

    则即则，

    .

    所以平面与平面所成二面角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：

    组号

    第一组

    第二组

    第三组

    第四组

    第五组

    分组

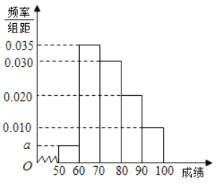
    （1）求图中的值；

    （2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；

    （3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥P－ABCD中，底面是边长为1的正方形，侧棱PD＝1，PA＝PC＝.

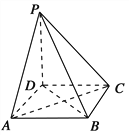
    （1）求证：PD⊥平面ABCD；

    （2）求证：平面PAC⊥平面PBD；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路和山区边界的直线型公路．记两条相互垂直的公路为，山区边界曲线为．计划修建的公路为，如图所示，为的两个端点，测得点到的距离分别为5千米和40千米，点到的距离分别为20千米和2．5千米，以所在直线分别为轴，建立平面直角坐标系．假设曲线符合函数（其中为常数）模型．

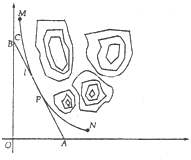
    （1）求的值；

    （2）设公路与曲线相切于点，的横坐标为．

    ①请写出公路长度的函数解析式，并写出其定义域；

    ②当为何值时，公路的长度最短？求出最短长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）当时，函数与的图象有三个不同的交点，求实数的范围；

    （2）讨论的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，点是直线上的一动点，过点作圆的切线，切点为．

    （1）当切线的长度为时，求点的坐标；

    （2）若的外接圆为圆，试问：当在直线上运动时，圆是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由．

    （3）求线段长度的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图．

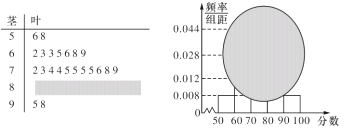
    （1）求分数在的频率及全班人数；

    （2）求分数在之间的频数，并计算频率分布直方图中间矩形的高；

    （3）若要从分数在之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】围建一个面积为360的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为（单位：），修建此矩形场地围墙的总费用为（单位：元）

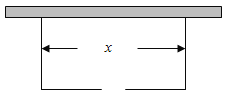
    （1）将表示为的函数；

    （2）试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况，对全年级2000名高三学生进行了问卷调查，统计结果如下表：

    校区

    愿意参加

    不愿意参加

    重庆一中本部校区

    220

    980

    重庆一中大学城校区

    80

    720

    （1）若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人，则大学城校区应抽取几人；

    （2）现对愿意参加自主招生的同学组织摸底考试，考试题共有5道题，每题20分，对于这5道题，考生“如花姐”完全会答的有3题，不完全会的有2道，不完全会的每道题她得分的概率满足：，假设解答各题之间没有影响，

    ①对于一道不完全会的题，求“如花姐”得分的均值；

    ②试求“如花姐”在本次摸底考试中总得分的数学期望．

    查看答案和解析>>

    同步练习册答案