练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若抛物线y2＝－2px(p>0)上有一点M，其横坐标为－9.它到焦点的距离为10，求抛物线方程和M点的坐标．

     

    【答案】

    y2＝－4x，M(－9,6)或M(－9，－6)

    【解析】本题考查抛物线的几何性质，解题时要认真审题，注意挖掘题设中的隐含条件。

    （1）（1）抛物线的开口向右，焦点在x轴的正半轴上，故可求焦点F坐标；

    （2）利用点A（-2，3）到抛物线y2=2px（p＞0）焦点F的距离为5，从而 利用定义故可求出抛物线的方程．

    解：由抛物线定义知焦点为F(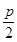－，0)，准线为x＝，

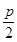    由题意设M到准线的距离为|MN|， 则|MN|＝|MF|＝10，  即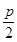－(－9)＝10，

    ∴p＝2.故抛物线方程为y2＝－4x，将M(－9，y)代入y2＝－4x，解得y＝±6，

    ∴M(－9,6)或M(－9，－6)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：辽宁省沈阳二中2011－2012学年高二上学期12月月考数学试题 题型：013

    设经过定点M(a，0)的直线与抛物线y2＝2px相交于P，Q两点，若为常数，则a的值为

    [　　]
    A．

    p

    B．

    2p

    C．

    D．

    －2p

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    已知抛物线y2＝2px（p＞0）.过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p.

    （Ⅰ）求a的取值范围；

    （Ⅱ）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    已知抛物线y2＝2px（p＞0）.过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p.

    （Ⅰ）求a的取值范围；

    （Ⅱ）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    已知抛物线y2＝2px(p＞0)，过动点M(a，0)且斜率为1的直线l与该抛物线交于不同的两点A、B，①若|AB|≤2p，求a的取值范围；②若线段AB的垂直平分线交AB于点Q，交x轴于点N，求直角三角形MNQ的面积．

    查看答案和解析>>

    科目：高中数学 来源：新课程高中数学疑难全解 题型：044

    如图所示，已知抛物线y2＝2px(p＞0)，过动点M(a，0)且斜率为1的直线l与该抛物线交于不同的两点A、B，且|AB|≤2p．

    (1)求a的取值范围；

    (2)若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值．

    查看答案和解析>>

    同步练习册答案