【答案】
分析:根据同角三角函数间的基本关系得出sin
2x+cos
2x=1,移项后变形为cos
2x=1-sin
2x,右边利用平方差公式分解因式,把积的恒等式变为比例形式,可得到已知的等式的左边与所求式子互为相反数,由已知等式的值即可求出所求式子的值.
解答:解:∵sin
2x+cos
2x=1,
∴cos
2x=1-sin
2x,
∴cosx•cosx=(1+sinx)(1-sinx),
即
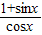
=
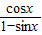
=-
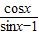
,
∵
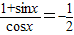
,
∴
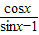
=

.
故答案为:
 点评:
点评:此题考查了同角三角函数间的基本关系的运用,学生做题时注意灵活运用“1”的变形,同时根据sin
2x+cos
2x=1变形为比例式,得出已知与未知的联系,达到解决问题的目的,其中对sin
2x+cos
2x=1的灵活变形是解本题的关键.

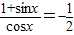 ,则
,则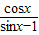 的值是 .
的值是 . 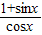 =
=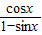 =-
=-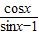 ,
,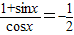 ,
,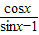 =
= .
.

