
【题目】已知椭圆E的中心在坐标原点O,两个焦点分别为A(﹣1,0),B(1,0),一个顶点为H(2,0).
(1)求椭圆E的标准方程;
(2)对于x轴上的点P(t,0),椭圆E上存在点M,使得MP⊥MH,求实数t的取值范围.
科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线方程为
l:y=3x+1,且当x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的为( )
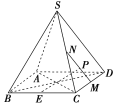
A.①③B.③④C.①②D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
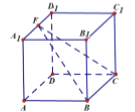
【题目】如图,在正方体![]() 中,
中,![]() 是棱
是棱![]() 上动点,下列说法正确的是( )
上动点,下列说法正确的是( )
A. 对任意动点![]() ,在平面
,在平面![]() 内不存在与平面
内不存在与平面![]() 平行的直线
平行的直线
B. 对任意动点![]() ,在平面
,在平面![]() 内存在与平面
内存在与平面![]() 垂直的直线
垂直的直线
C. 当点![]() 从
从![]() 运动到
运动到![]() 的过程中,
的过程中,![]() 与平面
与平面![]() 所成的角变大
所成的角变大
D. 当点![]() 从
从![]() 运动到
运动到![]() 的过程中,点
的过程中,点![]() 到平面
到平面![]() 的距离逐渐变小
的距离逐渐变小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() 在
在![]() 轴上,中心在坐标原点,长轴长为4,短轴长为
轴上,中心在坐标原点,长轴长为4,短轴长为![]() .
.
(1)求椭圆的标准方程;
(2)是否存在过![]() 的直线
的直线![]() ,使得直线
,使得直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD由Rt△ABC和Rt△BCD拼接而成,其中∠BAC=∠BCD=90°,∠DBC=30°,AB=AC,![]() ,将△ABC沿着BC折起,
,将△ABC沿着BC折起,
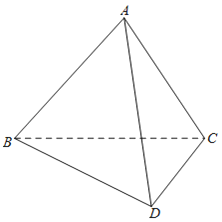
(1)若![]() ,求异面直线AB和CD所成角的余弦值;
,求异面直线AB和CD所成角的余弦值;
(2)当四面体ABCD的体积最大时,求二面角A﹣BC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆近年来旅游业高速发展,有很多著名景点,如洪崖洞、磁器口、朝天门、李子坝等.为了解端午节当日朝天门景点游客年龄的分布情况,从年龄在22~52岁之间的旅游客中随机抽取了1000人,制作了如图的频率分布直方图.

(1)求抽取的1000人的年龄的平均数、中位数;(每一组的年龄取中间值)
(2)现从![]() 中按照分层抽样抽取8人,再从这8人中随机抽取3人,记这3人中年龄在
中按照分层抽样抽取8人,再从这8人中随机抽取3人,记这3人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )

A.AC⊥BEB.EF![]() 平面ABCD
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com