
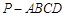 的底面ABCD为正方形,
的底面ABCD为正方形,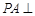 平面ABCD,E、F分别是BC,PC的中点,
平面ABCD,E、F分别是BC,PC的中点,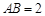 ,
,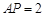 .
.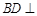 平面
平面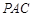 ;
;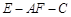 的大小.
的大小.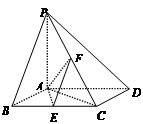
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源:不详 题型:解答题
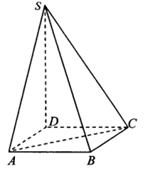
 平面ABCD,SD=2a,
平面ABCD,SD=2a,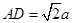 ,点E是SD上的点,且
,点E是SD上的点,且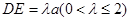
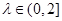 ,都有
,都有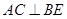
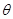
 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为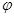 ,若
,若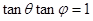 ,求
,求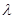 的值
的值查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
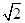 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
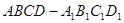 中,
中,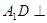 平面
平面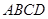 ,底面
,底面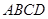 是边长为
是边长为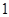 的正方形,侧棱
的正方形,侧棱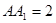 .
.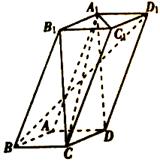
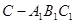 的体积;
的体积;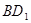 与平面
与平面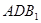 所成角的正弦值;
所成角的正弦值;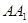 上存在一点
上存在一点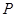 ,使得
,使得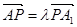 ,当二面角
,当二面角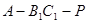 的大小为
的大小为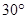 时,求实数
时,求实数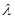 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
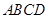 的三组对棱分别相等,即
的三组对棱分别相等,即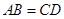 ,
,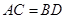 ,
,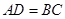 ,则________.(写出所有正确结论编号)
,则________.(写出所有正确结论编号) 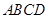 每组对棱相互垂直
每组对棱相互垂直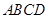 每个面的面积相等
每个面的面积相等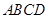 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于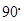 而小于
而小于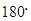
 每组对棱中点的线段互垂直平分
每组对棱中点的线段互垂直平分 每个顶点出发的三条棱的长可作为一个三角形的三边长
每个顶点出发的三条棱的长可作为一个三角形的三边长查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com